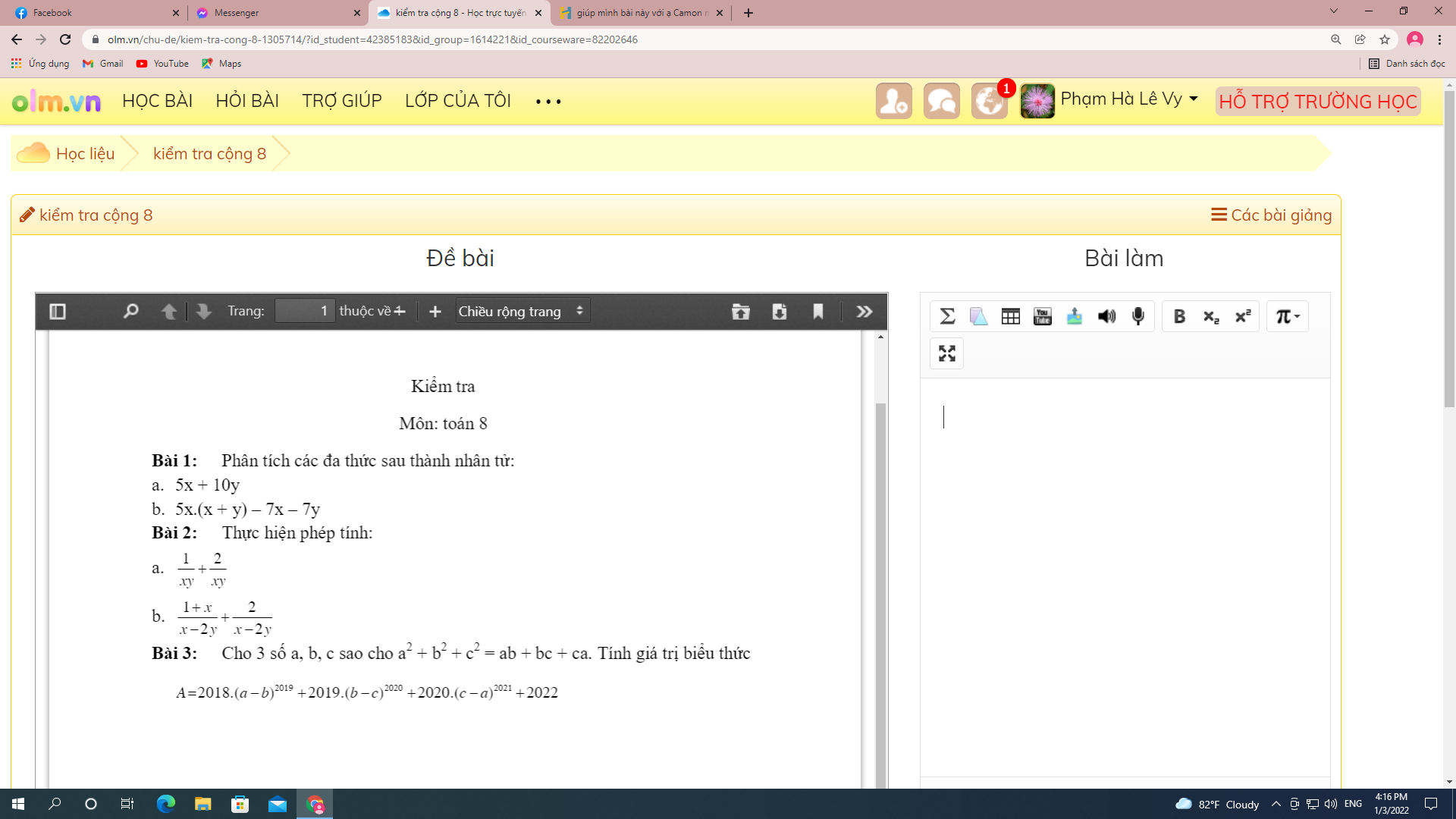
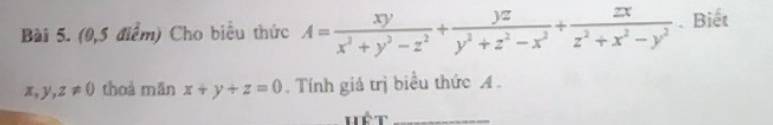\(\left(x+y\right)^2+\left(y+z\right)^2+\left(z+x\right)^2=12\)
\(\Leftrightarrow\left(x+y+z\right)^2+x^2+y^2+z^2=12\)
\(\Leftrightarrow x^2+y^2+z^2=3\)
Dễ dàng c/m : \(x^2+y^2+z^2\ge\dfrac{\left(x+y+z\right)^2}{3}\) \(\Rightarrow x^2+y^2+z^2\ge\dfrac{3^2}{3}=3\)
" = " \(\Leftrightarrow x=y=z=1\)
Khi đó : \(A=1^{2019}.3=3\)
Vậy ...