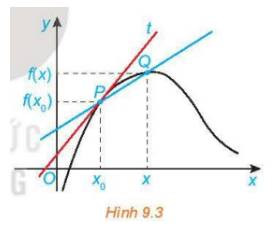
Với \({x_0}\) bất kì, ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{ - {x^2} + 4x + x_0^2 - 4{x_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{ - \left( {{x^2} - x_0^2} \right) + 4\left( {x - {x_0}} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( { - x - {x_0} + 4} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left( { - x - {x_0} + 4} \right) = - 2{x_0} + 4\)
Vậy hàm số \(y = - {x^2} + 4x\) có đạo hàm là hàm số \(y' = - 2x + 4\)
a) Ta có \(y'\left( 1 \right) = - 2.1 + 4 = 2\)
Ngoài ra , \(f\left( 1 \right) = 3\) nên phương trình tiếp tuyến cần tìm là:
\(y - 3 = 2\left( {x - 1} \right)\) hay \(y = 2x + 1\)
b) Ta có \({y_0} = 0\) nên \( - x_0^2 + 4{x_0} = 0 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 0\\{x_0} = 4\end{array} \right.\)
+) \({x_0} = 0,{y_0} = 0\) nên \(y'\left( 0 \right) = 4\) do đó phương trình tiếp tuyến cần tìm là \(y = 4x\)
+) \({x_0} = 4,{y_0} = 0\) nên \(y'\left( 4 \right) = - 4\) do đó phương trình tiếp tuyến cần tìm là
\(y = - 4\left( {x - 4} \right)\) hay \(y = - 4x + 16\)