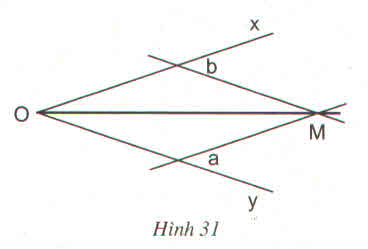
a) Sửa lại đề là \(CA=CB\) nhé.
Gọi \(Oz\) là tia phân giác của \(\widehat{xOy}.\)
Mà tia phân giác của \(\widehat{xOy}\) cắt \(AB\) tại \(C\left(gt\right)\)
=> \(OC\) là tia phân giác của \(\widehat{AOB}.\)
=> \(\widehat{AOC}=\widehat{BOC}.\)
Xét Δ AOC và Δ BOC có:
OA = OB (gt)
góc AOC = góc BOC (chứng minh trên)
OC là cạnh chung
=> Δ AOC = Δ BOC (c.g.c) (đpcm)
=> \(AC=BC\) (2 cạnh tương ứng).
b) Theo câu a) ta có \(\Delta AOC=\Delta BOC.\)
=> \(\widehat{ACO}=\widehat{BCO}\) (2 góc tương ứng).
Gọi I là giao điểm của \(AB\) và \(OC.\)
\(\widehat{ACO}=\widehat{BCO}\left(cmt\right)\)
=> \(\widehat{ACI}=\widehat{BCI}.\)
Xét Δ AIC và Δ BIC có:
AC = BC (chứng minh trên)
góc ACI = BCI (chứng minh trên)
CI là cạnh chung
=> Δ AIC = Δ BIC (c.g.c)
=> \(\widehat{AIC}=\widehat{BIC}\) (2 góc tương ứng).
Ta có: \(\widehat{AIC}+\widehat{BIC}=180^0\) (vì 2 góc kề bù).
=> \(\widehat{AIC}=\widehat{BIC}=\frac{180^0}{2}\)
=> \(\widehat{AIC}=\widehat{BIC}=90^0.\)
=> \(AB\perp IC.\)
Hay \(AB\perp OC\left(đpcm\right).\)
Chúc bạn học tốt!