Chương 1: HÀM SỐ LƯỢNG GIÁC. PHƯƠNG TRÌNH LƯỢNG GIÁC
Các câu hỏi tương tự
Vẽ đồ thị hàm số lượng giác
Giải giúp e vs ạ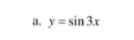
Từ đồ thị hàm số y=sinx , hãy vẽ đồ thị các hàm số sau :
a, y=-sinx
b, y=sin\(\left|x\right|\)
c, y=sinx +1
Tịnh tiến đồ thị hàm số y= cos x sang phải \(\dfrac{\pi}{2}\) ta được đồ thị hàm số nào
A. \(y=sinx\)
B.\(y=-cosx\)
C.\(y=\)\(cos\left(x+\dfrac{\pi}{2}\right)\)
D.\(y=sin\left(x-\dfrac{\pi}{2}\right)\)
Tìm giá trị của tham số k để đồ thị hàm số y = -2x + k(x+1) đi qua gốc tọa độ 0
6 tháng 9 2016 lúc 12:42
a)vẽ đồ thị hàm số ysin x rồi chỉ ra trên đồ thị đó các điểm có hoành độ thuộc khoảng left(-pi;4piright) là nghiệm của mõi phương trình sau : 1) sin x-frac{sqrt{3}}{2} ; 2) sin x1b) cũng câu hỏi tương tự cho hàm số ycos x đối với mỗi phương trình sau : 1) cos xfrac{1}{2} ; 2) cos x-1
Đọc tiếp
a)vẽ đồ thị hàm số \(y=\sin x\) rồi chỉ ra trên đồ thị đó các điểm có hoành độ thuộc khoảng \(\left(-\pi;4\pi\right)\) là nghiệm của mõi phương trình sau :
1) \(\sin x=-\frac{\sqrt{3}}{2}\) ; 2) \(\sin x=1\)
b) cũng câu hỏi tương tự cho hàm số \(y=\cos x\) đối với mỗi phương trình sau : 1) \(\cos x=\frac{1}{2}\) ; 2) \(\cos x=-1\)
6 tháng 9 2016 lúc 12:46
a)vẽ đồ thị hàm số ytan x rồi chỉ ra trên đồ thị đó các điểm có hoành độ thuộc khoảng left(-pi;piright) là nghiệm của mõi phương trình sau : 1) tan x-1 ; 2) tan x0b) cũng câu hỏi tương tự cho hàm số ycot x đối với mỗi phương trình sau : 1) cot xfrac{sqrt{3}}{3} ; 2) cot x1
Đọc tiếp
a)vẽ đồ thị hàm số \(y=\tan x\) rồi chỉ ra trên đồ thị đó các điểm có hoành độ thuộc khoảng \(\left(-\pi;\pi\right)\) là nghiệm của mõi phương trình sau :
1) \(\tan x=-1\) ; 2) \(\tan x=0\)
b) cũng câu hỏi tương tự cho hàm số \(y=\cot x\) đối với mỗi phương trình sau : 1) \(\cot x=\frac{\sqrt{3}}{3}\) ; 2) \(\cot x=1\)
30 tháng 8 2016 lúc 18:51
cho hàm số y f(x) 2sin2x .a) chứng minh rằng với số nguyên k tùy ý , luôn có f(x + kpi) f(x) với mọi x .b) lập bảng biến thiên của hàm số y 2sin2x trên đoạn left[-frac{pi}{2};frac{pi}{2}right]c) vẽ đồ thị của hàm số y 2sin2x .
Đọc tiếp
cho hàm số y = f(x) = 2\(\sin\)2x .
a) chứng minh rằng với số nguyên k tùy ý , luôn có f(x + k\(\pi\)) = f(x) với mọi x .
b) lập bảng biến thiên của hàm số y = 2\(\sin\)2x trên đoạn \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
c) vẽ đồ thị của hàm số y = 2\(\sin\)2x .
1. dựa vào đồ thị hàm số y = sinx , hãy vẽ đồ thị hàm số :
a, y = |sinx|
b. y = sin |x|
c.y = sinx + 2
d. \(y=sin\left(x+\pi\right)\)
Giải hàm số lượng giác sau:
\(\dfrac{sin2x-2sinx}{sin2x+2sinx}\)