xét tam giác ABC có :
EA = FB (gt)
FB = FC (gt)
\(\Rightarrow EF\) là đường trung bình
\(\Rightarrow\) EF // AC và EF = \(\dfrac{1}{2}\) AC (1)
chứng minh tương tự HG là đường trung bình tam giác ADC
HG // AC và HG = \(\dfrac{1}{2}\) AC (2)
từ (1) và (2) ta suy ra EF // HG và EF = HG
\(\Rightarrow\) EFGH là hình bình hành (3)
ta có : EF // AC
EH // BD ( EH là đường trung bình tam giác ABD )
AC \(\perp\) BD ( gt )
\(\Rightarrow\) EF \(\perp\) EH
hay góc E = 90 độ (4)
từ (3) và (4) ta suy ra EFGH là hình chữ nhật

Bài giải:
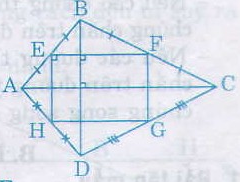
Ta có EB = EA, FB = FC (gt)
Nên EF là đường trung bình của ∆ABC
Do đó EF // AC
HD = HA, GD = GC
Nên HG là đường trung bình của ∆ADC
Do đó HG // AC
Suy ra EF // HG
Tương tự EH // FG
Do đó EFGH là hình bình hành.
EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH hay ˆFEHFEH^ = 900
Hình bình hành EFGH có ˆEE^ = 900 nên là hình chữ nhật.








