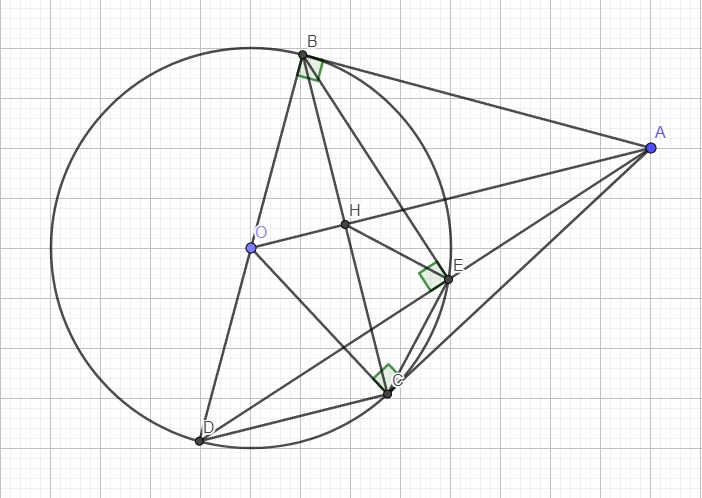
Từ điểm A nằm ngoài đường tròn (O;R), vẽ 2 tiếp tuyến AB,AC với đường tròn (B,C là tiếp điểm). Gọi H là giao điểm của OA và BC. ( VẼ HÌNH HỘ MÌNH NHÉ) a) Cm: 4 điểm A,B,O,C cùng thuộc 1 đg tròn (CM theo 2 tam giác nội tiếp) b) Kẻ đg kính BD. Gọi E là giao điểm của đoạn thẳng AD với (O), E ko trùng với D. Cm: DE/BE=BD/BA và tính góc HEC
a.
Do AB là tiếp tuyến của (O) \(\Rightarrow AB\perp OB\Rightarrow\Delta ABO\) vuông tại B
\(\Rightarrow\Delta ABO\) nội tiếp đường tròn đường kính OA (1)
Tương tự, do AC là tiếp tuyến của (O) \(\Rightarrow\Delta ACO\) vuông tại C
\(\Rightarrow\Delta ACO\) nội tiếp đường tròn đường kính OA (2)
(1);(2) \(\Rightarrow\)4 điểm A,B,O,C cùng thuộc đường tròn đường kính OA
b.
Do BD là đường kính và E là điểm thuộc đường tròn nên \(\widehat{BED}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{BED}=90^0\)
Xét hai tam giác EAB và EBD có:
\(\left\{{}\begin{matrix}\widehat{AEB}=\widehat{BED}=90^0\\\widehat{EBA}=\widehat{EDB}\left(\text{cùng phụ }\widehat{EBD}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta EAB\sim\Delta EBD\left(g.g\right)\Rightarrow\dfrac{DE}{BE}=\dfrac{BD}{AB}\)
//\(\widehat{BCD}\) là góc nội tiếp chắn nửa đường tròn \(\Rightarrow\widehat{BCD}=90^0\)
Do \(AB=AC\) (t/c hai tiếp tuyến cắt nhau) và \(OB=OC=R\)
\(\Rightarrow OA\) là trung trực của BC \(\Rightarrow OA\perp BC\) tại H
Xét hai tam giác BCD và AHB có:
\(\left\{{}\begin{matrix}\widehat{BCD}=\widehat{AHB}=90^0\\\widehat{ABC}=\widehat{BDC}\left(\text{cùng chắn cung BC}\right)\end{matrix}\right.\) \(\Rightarrow\Delta BCD\sim\Delta AHB\left(g.g\right)\)
\(\Rightarrow\dfrac{BD}{AB}=\dfrac{CD}{BH}\Rightarrow\dfrac{CD}{BH}=\dfrac{DE}{BE}\)
Xét hai tam giác CDE và BHE có:
\(\left\{{}\begin{matrix}\dfrac{CD}{BH}=\dfrac{DE}{BE}\\\widehat{CDE}=\widehat{HBE}\left(\text{cùng chắn }CE\right)\end{matrix}\right.\) \(\Rightarrow\Delta CDE\sim\Delta BHE\left(g.g\right)\)
\(\Rightarrow\widehat{CED}=\widehat{BEH}\)
Mà \(\widehat{BEH}+\widehat{DEH}=\widehat{BED}=90^0\)
\(\Rightarrow\widehat{HEC}=\widehat{CED}+\widehat{DEH}=90^0\)
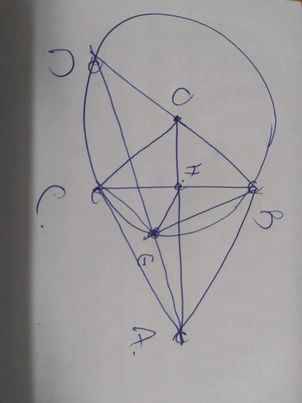
a: Ta có: ΔOBA vuông tại B
=>B,O,A cùng nằm trên đường tròn đường kính OA(1)
Ta có: ΔOCA vuông tại C
=>O,C,A cùng nằm trên đường tròn đường kính OA(2)
Từ (1) và (2) suy ra B,O,A,C cùng thuộc một đường tròn
b: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔEBD vuông tại E và ΔEAB vuông tại E có
\(\widehat{EBD}=\widehat{EAB}\left(=90^0-\widehat{BDA}\right)\)
Do đó: ΔEBD~ΔEAB
=>\(\dfrac{ED}{EB}=\dfrac{BD}{AB}\)