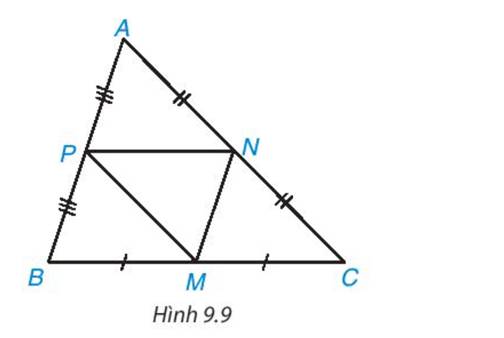
- Có AP = BP, NA = NC
=> NP // BC (P ∈ AB, N ∈ AC)
=> ΔABC \(\backsim\) ΔAPN
- Có AP = BP, MB = MC
=> MP // AC (P ∈ AB, M ∈ BC)
=> ΔABC \(\backsim\) ΔPBM
- Có NA = NC, MB = MC
=> MN // AB (N ∈ AC,M ∈ BC)
=> ΔABC \(\backsim\) ΔNMC
- Có ΔABC \(\backsim\) ΔAPN và ΔABC \(\backsim\) ΔPBM => ΔAPN \(\backsim\) ΔPBM
- Có ΔABC \(\backsim\) ΔNMC và ΔABC \(\backsim\) ΔPBM => ΔNMC \(\backsim\) ΔPBM