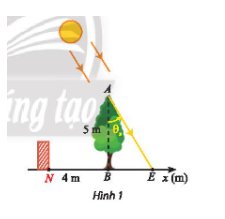
Trong Hình 1, cây xanh AB nằm trên đường xích đạo được trồng vuông góc với mặt đất và có chiều cao 5 m. Bóng của cây là BE. Vào ngày xuân phân và hạ phân, điểm E di chuyển trên đường thẳng Bx. Góc thiên đỉnh \({\theta _t} = (AB,AE)\) phụ thuộc vào vị trí của Mặt trời và thay đổi theo thời gian trong ngày theo công thức \({\theta _s}(t) = (AB,AE) = \frac{\pi }{{12}}(t - 12)\;\) rad với t là thời gian trong ngày (theo đơn vị giờ, 6 < t < 18).
(Theo https://www.sciencedirect.com/topics/engineering/solar-hour-angle)
a) Viết hàm số biểu diễn toạ độ của điểm E trên trục Bx theo t.
b) Dựa vào đồ thị hàm số tang, hãy xác định các thời điểm mà tại đó bóng cây phủ qua vị trí tường rào N biết N nằm trên trục Bx với toạ độ là \({x_N} = - 4\;\) (m). Làm tròn kết quả đến hàng phần mười.
a, Xét tam giác ABE vuông tại B, ta có:
\(tan\theta_s\left(t\right)=\dfrac{BE}{AB}\Leftrightarrow BE=5tan\left[\dfrac{\pi}{12}\left(t-12\right)\right]\)
b, Đồ thị của hàm số \(\theta_s=5tan\left[\dfrac{\pi}{12}\left(t-12\right)\right]\)
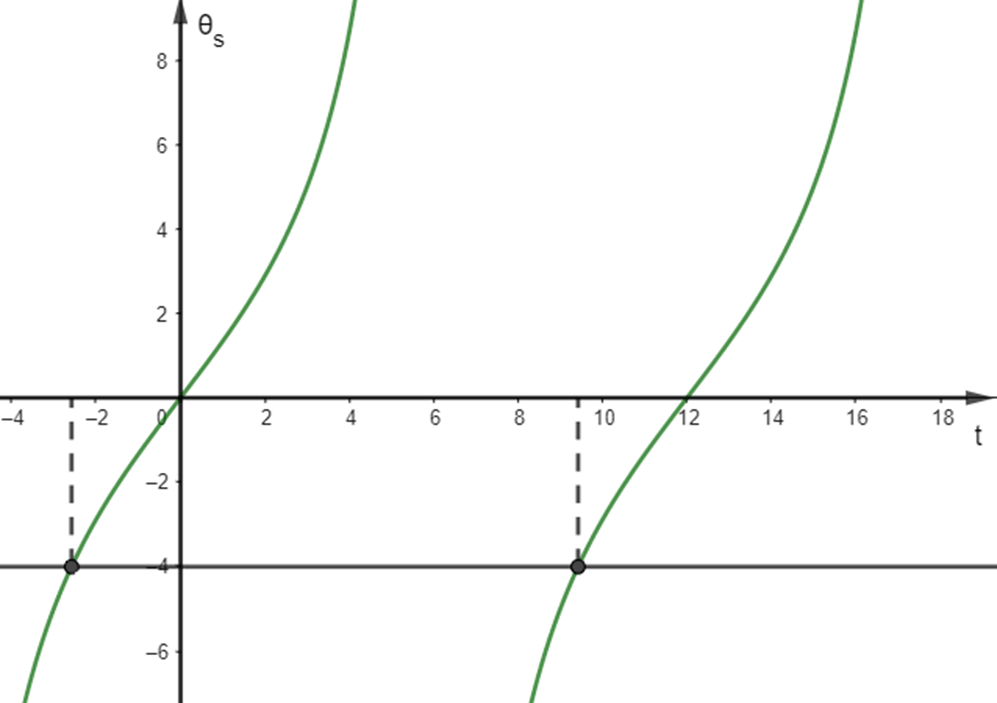
Dựa vào đồ thị hàm số, ta có:
\(\theta_s=5tan\left[\dfrac{\pi}{12}\left(t-12\right)\right]< -4\\ \Leftrightarrow tan\left[\dfrac{\pi}{12}\left(t-12\right)\right]< -\dfrac{4}{5}\\ \Leftrightarrow\dfrac{\pi}{12}\left(t-12\right)< -0,67\\ \Leftrightarrow t< 9,4\)
Kết hợp điều kiện \(6< t< 18\Rightarrow6< t< 9,4\)
Vậy thời điểm bóng cây phủ qua hàng rào là 6 < t < 9,4.






