Question

Trên hình 90, ta có OA = OB, ∠OAC = ∠OBD. Chứng minh:

a) ∠ODB = ∠OCA;

b) ID = IC;

c) OI là phân giác của góc DOC và OI \(\perp\) CD

Answer 1

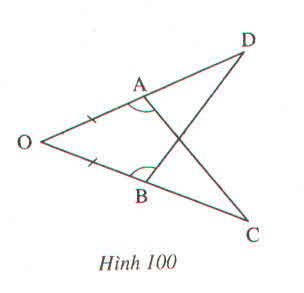
a, xét △OBD và △OAC có :

∠O chung

OA=OB(gt)

∠OAC=∠OBD

do đó △OBD = △OAC(g.c.g)

=> ∠ODB=∠OAC(2 góc tương ứng)(đpcm)

b, Ta có : OAC+DAI=180^o

OBD+CBD=180^o(2 góc kề bù)

mà OAC=OBD (gt|)

=> DAI=CGB

Lại có : OB+BC=OC

OA+AD=OD

mà OB=OA,OD=OC ( do △OBD và △OAC)

=> BC=AD

Xét △AID và △BIC có :

DAI=CGB

BC=AD

D=C( do △OBD và △OAC)

=>△AID = △BIC(g.c.g)

=>ID=IC(2 cạnh tương ứng)(đpcm)

c, *,vì AI+IC=AC

BI+ID=BD

mà IB=IC ( do △AID và △BIC)

AC=BD( do △OBD và △OAC)

nên AI=BI

xét △OAI và △OBI có :

OA=OB(gt)

OAI=OBI(gt)

AI=BI(cmt)

=>△OAI = △OBI(c.g.c)

=>AOI=BOI(2 cạnh tương ứng)

=>OI là tia p/g AOI hay OI là tia p/g BOD

*, Gọi K là gđ của OI với BD

xét △OKD và △OKB có :

OD+OB

OAI=OBI

OK chung

=>△OKD = △OKB(cgc)

=>OKD=OKB(2 cạnh tương ứng)

mà OKD +OKB =180^o(2 góc kb)

=> OKD=OKB=180⁰/2=90^o

=>OK⊥DB hay OI⊥DB