Xem thêm công thức tính các loại diện tích tam giác tại đây: https://7scv.com/bai/cong-thuc-tinh-dien-tich-tam-giac-chuan-nhat.13958/
Bài 3: Diện tích tam giác
Các câu hỏi tương tự
a) Có thể dùng kéo cắt 2 lầ và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh đê rghesp lại được một hình chữ nhật hay không ?
Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật
b) Hãy chia một tam giác thành 2 phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó
c) Hãy chia một tam giác thành 4 phần có diện tích bằng nhau bởi ba đường thẳng, trong đó chỉ có một đường đi qua đỉnh của tam giác đó
Đọc tiếp
a) Có thể dùng kéo cắt 2 lầ và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh đê rghesp lại được một hình chữ nhật hay không ?
Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật
b) Hãy chia một tam giác thành 2 phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó
c) Hãy chia một tam giác thành 4 phần có diện tích bằng nhau bởi ba đường thẳng, trong đó chỉ có một đường đi qua đỉnh của tam giác đó
Cho tam giác ABC. Một đường thẳng song song với BC cắt AB, AC theo thứ tự ở D và E. Gọi G là một điểm nằm trên BC. Tính diện tích tứ giác ADGE biết diện tích tam giác ABC bằng 16 cm vuông, diện tích tam giác ADE bằng 9cm vuông
Chứng minh rằng ba trung tuyến của một tam giác chia tam giác đó thành 6 hình tam giác có diện tích bằng nhau
GIÚP VỚI
giải chi tiết nha
Cho tam giác ABC. Lấy các điểm D, E, F thứ tự thuộc các cạnh
AB, BC, CA sao cho AD=1/3*AB, BE=1/3*BC, CF=1/3*CA. Các đoạn thẳng AE, BF, CD cắt nhau tạo thành một tam giác. Chứng minh rằng diện tích tam giác này bằng 1/7 diện tích tam giác ABC.
Hai đường chéo của hình chữ nhật chia hình chữ nhật thành 4 tam giác. Diện tích của các tam giác đó có bằng nhau không ? Vì sao ?
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S là diện tích của tam giác DBC
Chứng minh rằng : dfrac{S}{S}dfrac{DK}{AH}
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và son...
Đọc tiếp
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S' là diện tích của tam giác DBC
Chứng minh rằng : \(\dfrac{S'}{S}=\dfrac{DK}{AH}\)
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T
Chứng minh rằng \(\dfrac{MH}{AD}+\dfrac{MK}{BE}+\dfrac{MT}{CF}=\)
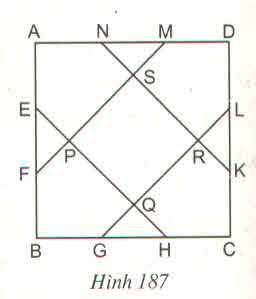
Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD thành 3 đoạn thẳng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL (h.187). Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS, biết AB = 6cm
cho hình thang abcd (ab//cd) gọi f là giao điểm của hai chéo ac và bd a) chứng minh tam giác fcd b) chứng minh fa. fd =fb.fc c) đường thẳng f vuông góc với ab tại m và cắt cd tại n , biết fb =2cm , fd= 4cm ,fm=3cm , cd=8cm hãy tính diện tích tam giác fdc
Cho tam giác ABC có chu vi là 10 cm, giao điểm I của các đường phân giác các cạnh 1 cm. Tính diện tích tam giác ABC








