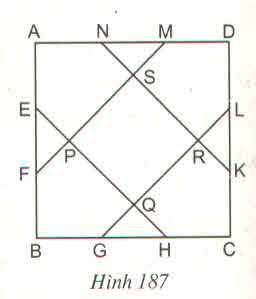
Diện tích hình vuông \(ABCD\) : \(\dfrac{1}{2}\times4\times4=8\left(cm^2\right)\)
Diện tích \(\Delta DKN\) : \(\dfrac{1}{2}\times4\times4=8\left(cm^2\right)\)
Diện tích phần còn lại là: \(36-\left(8+8\right)=20\left(cm^2\right)\)
Trong \(\Delta\) vuông \(AEN\) ta có:
\(EN^2=AN^2+AE^2=4+4=8\)
\(EN=\sqrt{8}=2\sqrt{2}\left(cm\right)\)
Trong \(\Delta\) vuông \(BHE\) ta có:
\(EH^2=BE^2+BH^2=16+16=32\)
\(EH=\sqrt{32}=4\sqrt{2}\left(cm\right)\)
\(S_{ENKH}=2\sqrt{2}\times4\sqrt{2}=16\left(cm^2\right)\)
Nối đường chéo \(BD\). Théo tính chất đường thẳng song song cách đều ta có hình chữ nhật \(ENKH\) chia thành bốn phần bằng nhau nên \(S_{PQRS}\) chiếm 2 phần bằng \(8cm^2\) .
\(S_{AEPSN}=S_{AEN}+S_{EPSN}=2+\dfrac{16}{4}=6\left(cm^2\right)\)
Vậy............
Bài 3: Diện tích tam giác
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
cho hình thang abcd (ab//cd) gọi f là giao điểm của hai chéo ac và bd a) chứng minh tam giác fcd b) chứng minh fa. fd =fb.fc c) đường thẳng f vuông góc với ab tại m và cắt cd tại n , biết fb =2cm , fd= 4cm ,fm=3cm , cd=8cm hãy tính diện tích tam giác fdc
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S là diện tích của tam giác DBC
Chứng minh rằng : dfrac{S}{S}dfrac{DK}{AH}
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và son...
Đọc tiếp
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S' là diện tích của tam giác DBC
Chứng minh rằng : \(\dfrac{S'}{S}=\dfrac{DK}{AH}\)
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T
Chứng minh rằng \(\dfrac{MH}{AD}+\dfrac{MK}{BE}+\dfrac{MT}{CF}=\)
Cho tam giác ABC, gọi D, E, F lần lượt là trung điểm của các cạnh AB, AC,BC; và M, N, P, Q theo thứ tự là trung điểm của các đoạn thẳng DA, AE, EF, FD.
a) Chứng minh : EF là đường trung bình của tam giác ABC
b) Chứng minh : Các tứ giác DAEF;MNPQ là hình bình hành
c) Khi tam giác ABC vuông tại A thì các tứ giác DAEF; MNPQ là hình gì? Chứng minh?
Cho tam giác ABC. Một đường thẳng song song với BC cắt AB, AC theo thứ tự ở D và E. Gọi G là một điểm nằm trên BC. Tính diện tích tứ giác ADGE biết diện tích tam giác ABC bằng 16 cm vuông, diện tích tam giác ADE bằng 9cm vuông
Cho tam giác ABC có diện tích S. Gọi M, N là trung điểm của AB và AC.a)Tứ giác MNCB là hình gì ?b)Tính diện tích MNCD theo S
Cho tam giác ABC cân tại a có đường cao AH(H €BC).Gọi D là trung điểm của đoạn thẳng AB.Gọi K là điểm đối xứng với điểm H qua D
a, Chứng minh tứ giác AHBK là hình chữ nhật
b,Cho AH=9cm,BC=16cm.Tính diện tích tam giác ADH
c,Trên tia đối của tia HA lấy điểm E.Kẻ HF vuông góc với EC(F € EC). Gọi M,N lần lượt là trung điểm của HF, FC.Chứng minh rằng :BF vuông góc với EM
Cho tam giác ABC vuông tại A. Gọi E,Q lần lượt là trung điểm của BC,BA. Lấy F là điểm đối xứng với E qua Q.
a, C/m tam giác AEBF là hình thoi.
b, Cho AC=3 cm;BC=5cm. Tính diện tích tam giác ABC. c, Tìm điều kiện của tam giác ABC để AEBF là hình vuông. MONG MN GIÚP MIK VỚI Ạ, MIK CẦN GẤP. MIK CẢM ƠN Ạ 🥺🥺
cho hình chữ nhật ABCD , H là hình chiếu của B lên AC.Lấy M là trung điểm của AH, N là trung điểm của BH.Qua M kẻ đường thẳng vuông góc với BM cắt D tại K. Chứng minh rằng tứ giác MKCN là hình bình hành
Cho hình vuông ABCD, trên các cạnh AB,BC,CD,DA lần lượt lấy các điểm M,N,P,Q sao cho AM=BN=CP=DQ=\(\dfrac{1}{3}\)AB
a) Chứng minh SAMQ=SBMN=SCNP=SDPQ
b)Chứng minh tứ giác MNPQ là hình vuông
c)Tính cạnh hình vuông ABCD biết SMNPQ=100cm2
Ai giúp mik với mik đg cần gấp ạ