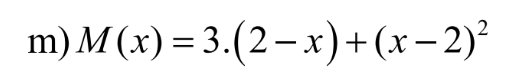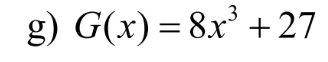Đặt \(M\left(x\right)=0\Rightarrow3.\left(2-x\right)+\left(x-2\right)^2=0\)
\(\Rightarrow-3.\left(x-2\right)+\left(x-2\right)^2=0\)
\(\Rightarrow\left(x-2\right).\left[\left(-3\right)+\left(x-2\right)\right]=0\\ \Rightarrow\left(x-2\right).\left(x-2-3\right)=0\\ \Rightarrow\left(x-2\right).\left(x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x-5=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
Vậy \(M\left(x\right)\) có nghiệm là \(x=2,x=5\).
`M(x)=3.(2-x)+(x-2)^2`
Ta có :
`3.(2-x)+(x-2)^2=0`
`=>3.(2-x)+(2-x)^2=0`
`=>(2-x).(3+2-x)=0`
`=>(2-x).(5-x)=0`
\(\Rightarrow\left[{}\begin{matrix}2-x=0\\5-x=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)