\(\Leftrightarrow x^3-3x^2+5=m\)
Xét hàm \(f\left(x\right)=x^3-3x^2+5\)
\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
BBT:
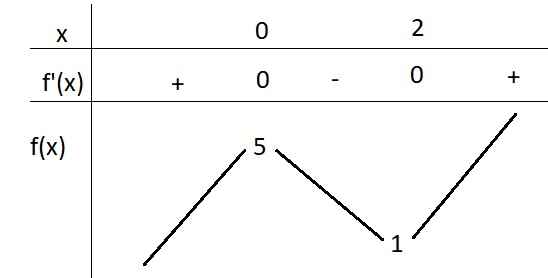
Từ BBT ta thấy \(y=m\) cắt \(y=f\left(x\right)\) tại 3 điểm khi \(1< m< 5\)
\(\Leftrightarrow x^3-3x^2+5=m\)
Xét hàm \(f\left(x\right)=x^3-3x^2+5\)
\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
BBT:

Từ BBT ta thấy \(y=m\) cắt \(y=f\left(x\right)\) tại 3 điểm khi \(1< m< 5\)
Tìm m để pt x^4-2x^2+3m-1=0 có 4 nghiệm phân biệt 🤔
Cho phương trình : 2|x|^3 - 9x^2 + 12 |x| + m = 0 (1)
Tìm m để (1) có : 6 nghiệm , 5 nghiệm , 4 nghiệm , 3 nghiệm , 2 nghiệm , 1 nghiệm , 0 nghiệm
Cho phương trình: 34x-2.32x=m. Tìm giá trị m để pt có 2 nghiệm phân biệt?
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
\( f(x)=\dfrac{1}{2}x^4-3x^2+\dfrac{3}{2}\)
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là nghiệm của phương trình \(f’’(x) = 0\)
c) Biện luận theo tham số \(m\) số nghiệm của phương trình: \(x^4 – 6x^2 + 3 = m\)
Tìm tất cả các giá trị thực của tham số m để hs y = (m+1).x^4 - mx^2 +3 có 3 điểm cực trị.
Tìm tất car các giá trị thực của tham số m để hs y= \(\dfrac{m}{3}.x^3-\left(m+1\right).x^2+\left(m-2\right).x-3m\) nghịch biến trên R.
Câu 1: Tìm điểm M thuộc đò thị(c): \(y= x^3-3x^2-2\) biết hệ số góc của tiếp tuyến với (c) tại M bằng 9
A.M(1;-6),M(-3;-2) B.M(-1;-6),M(3;-2) C.M(-1;-6),M(-3;-2) D.M(1;6),M(3;2)
Câu 2: Tiếp tuyến với đồ thị hàm số \(y=\frac{1}{3}x^3-2x^2+3x+4\) biết tiếp tuyến song song với đt d:y= \(3x-\frac{20}{3}\) là:
A.y=3x+4;y=\(3x-\frac{20}{3}\) B.y=3x-4;y=\(3x-\frac{40}{3}\) C.y=3x+4 D.y=3x-4
Câu 3: có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (0;10) đẻ đường thẳng d:y=-x+m cắt đò thị hàm số \(y=\frac{2x+1}{x-1}\)tại hai điểm phan biệt
A.5 B.6 C.7 D.8
Câu 4: Đặt a=log126, b=log12 7. Hãy biểu diễn log27 theo a và b
\(A.\frac{a}{b+1} B.\frac{b}{1-a} C.\frac{a}{b-1} D.\frac{b}{a+1}\)
Tập hợp tất cả các giá trị thực của tham số m để hs y= \(\dfrac{-1}{3}x^3+x^2+mx-2019\) nghịch biến trên khoảng (0 ; dương vô cùng)
bài 1: f=(m-1)/3 X3 - (m-1)x^2 -(m+4)x +m2 . Tìm m để f'(x) >= 0 có nghiệm?
bài 2: cho S.ABCD có đáy ABCD là hình vuông cạnh 2a. SAB là tam giác đều có đường cao SH; SH vuông góc vs (ABCD); góc anpha là góc [ BD; (SAD)] . Tìm góc anpha?
bài 3:cho S.ABCD có đáy ABCD là hình vuông cạnh a. SAB là tam giác đều có đường cao SH; SH vuông góc vs (ABCD); góc anpha là góc [ BD; (SAD)] . Tìm góc anpha?
(HELP ME)