A=căn x(căn x+2)-2022>=-2022
Dấu = xảy ra khi x=0
A=căn x(căn x+2)-2022>=-2022
Dấu = xảy ra khi x=0
C=2x-6 căn x+1(với x lớn hơn hoặc=0)
1. Giải các phương trình sau
căn x^2-2x+1 + căn x^2-4x+4 = 3
2. Tìm giá trị nhỏ nhất của các biểu thức sau
a, P= (căn 4x^2-4x+1) + (căn 4x^2-12x+9)
b, Q= (căn 49x^2-42x+9) + (căn 49x^2+42x+9)
Tìm các giá trị của x để biểu thức sau có nghĩa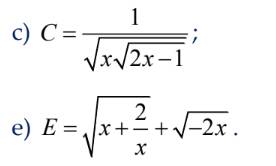
giúp mình với
căn bậc hai của (5-2căn bậc hai của 6)^2-căn bậc hai của (5+2căn bậc hai của 6)^2
a) chứng minh: \(\sqrt{a^2}+\sqrt{b^2}>\sqrt{\left(a+b\right)^2}\)
b) Tìm min của A=\(\sqrt{\left(2021-x\right)^2}+\sqrt{\left(2022-x\right)^2}\)
cho biết x + y = \(\sqrt{10}\)
tính giá trị nhỏ nhất của P = x2 + y2
tìm giá trị nhỏ nhất của biểu thức sau:
A=\(\frac{1}{2}\sqrt{x^2}+\sqrt{x^2-2x+1}\)
(2-căn x-1phần 2căn x-3):(6căn x+1phần 2x -căn x -3+cănx phần căn x +1)a, rút gon btb, tính gt của bt khi x=4b,so sánh với 3phần2
a ) Chứng tỏ rằng : \(x-2\sqrt{x}+17>0\) với mọi \(x\ge0\)
b ) Tìm giá trị nhỏ nhất của \(x-5\sqrt{x}-2018\)
Tìm giá trị nhỏ nhất √x^2+4x+4 + √x^2-4x+4