1. Gọi q(x)= ax3+bx2+cx+d
Ta có: q(0)= a.0+b.0+c.0+d=0
=> d=0
Vậy q(x) có 1 ngiệm là 0 khi a,b,c thuộc Q và d=0
1. Gọi q(x)= ax3+bx2+cx+d
Ta có: q(0)= a.0+b.0+c.0+d=0
=> d=0
Vậy q(x) có 1 ngiệm là 0 khi a,b,c thuộc Q và d=0
Ai đúng ? Ai sai ?
Bạn Đức đố : " Bậc của đa thức \(M=x^6-y^5+x^4y^4+1\) bằng bao nhiêu ?"
Bạn Thọ nói : "Đa thức M có bậc là 6"
Bạn Hương nói : "Đa thức M có bậc là 5"
Bạn Sơn nhận xét : "Cả hai bạn đều sai"
Theo em, ai đúng ? ai sai ? vì sao ?
Bài 1: Cho đa thức P(x) và Q(x) là các đơn thức thỏa mãn:
P(x) + Q(x) = x3+x2-4x+2 và P(x) - Q(x) = x3-x2+2x-2
a) Xác định đa thức P(x) và Q(x)
b) Tìm nghiệm của đa thức P(x) và Q(x)
c) Tính giá trị của P(x) và Q(x) biết |x- |\(\dfrac{x}{2}\)- |x-1||| = x-2
Bài 2: Biết rằng P(x) = n.xn+4+ 3.x4-n- 2x3+ 4x- 5 và Q(x) = 3.xn+4- x4+ x3+ 2nx2+ x- 2 là các đa thức với n là 1 số nguyên. Xác định n sao cho P(x) - Q(x) là 1 đa thức bậc 5 và có 6 hạng tử
Bài 3: Cho đa thức P(x) = x+ 7x2- 6x3+ 3x4+ 2x2+ 6x- 2x4+ 1
a) Thu gọn đa thức rồi sắp xếp các số hạng của đa thức theo lũy thừa giảm dần của biến x
b) Xác định bậc của đa thức, hệ số tự do, hệ số cao nhất
c) Tính P(-1); P(0); P(1); P(-a)
Bài 4: Cho đa thức bậc hai P(x) = ax2+ bx+ c với a ≠ 0
a) Chứng tỏ rằng nếu đa thức có nghiệm x = 1 thì sẽ có nghiệm x = \(\dfrac{c}{a}\)
b) Chứng tỏ rằng nếu đa thức có nghiệm x = -1 thì sẽ có nghiệm x = -\(\dfrac{c}{a}
\)
Cho đa thức P = ax4y3 + 10xy2 + 4y3 - 2x4y3 - 3xy2 + bx3y4
Biết rằng a,b là hằng và đa thức + có bậc 3; hãy tìm a và b
tìm đa thức bậc nhất P(x) biết rằng P(1)=5 và P(-1)=1
Cho đa thức \(A=2xy+\dfrac{1}{2}x^3y^2-xy-\dfrac{1}{2}x^3y^2+y-1\)
a) Thu gọn A. Tìm bậc của đa thức A
b) Tính giá trị biểu thức A tại x = 0,1 và y = -2.
Cho đa thức \(Q=-3x^5-\dfrac{1}{2}x^3y-\dfrac{3}{4}xy^2+3x^5+2\)
a) Thu gọn đa thức \(Q\)
b) Tìm bậc của đa thức Q
Cho đa thức f(x) = ax^2 + bx + c
chứng tỏ rằng a+b +c =0 thì đa thức f(x) có 1 nghiệm = 1
b áp dụng tìm 1 nghiệm của đa thức f(x) = 5x^2 -6x +1
Cho đa thức: A = \(-2xy^2+\dfrac{1}{3}x^3y-x-\dfrac{1}{3}x^3y+xy^2+x-4x^2y\). Thu gọn A và tìm bậc của A
Xác định bậc, hệ số tự do, hệ số cao nhất, của đa thức
P(x)=
Đáp án: Bậc của đa thức là: Trả lời
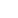
Hệ số tự do của đa thức là: Trả lời
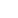
Hệ số cao nhất của đa thức là: