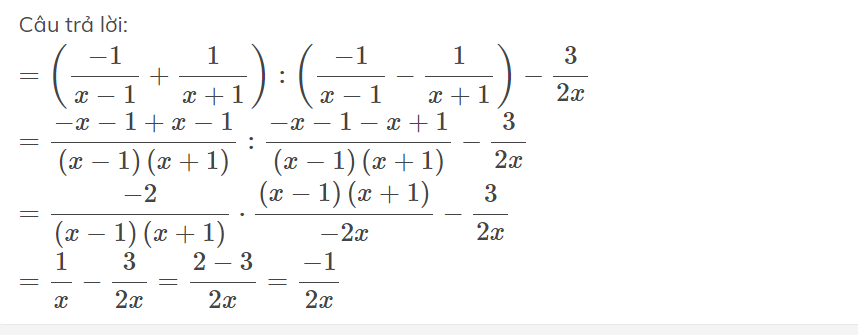Ôn tập toán 8
Các câu hỏi tương tự
Rút gọn : \(\left(\frac{1}{1-x}+\frac{1}{1+x}\right)\div\left(\frac{1}{1-x}-\frac{1}{1+x}\right)-\frac{3}{2x}\)
a) Rút gọn:
P = \(\left(2-\frac{x-1}{2x-3}\right)\div\left(\frac{6x+1}{2x^2-x-3}+\frac{x}{x+1}\right)\)
b) So sánh P với \(\frac{3}{2}\)
Rút gọn A = \(\left[\left(1+\frac{1}{x^2}\right)\div\left(1+2x+x^2\right)+\frac{2}{\left(x+1\right)^3}\left(1+\frac{1}{x}\right)\right]\div\frac{x-1}{x^3}\)
Tìm tập xác định
Rút gọn A = \(\left[\left(1+\frac{1}{x^2}\right)\div\left(1+2x+x^2\right)+\frac{2}{\left(x+1\right)^3}\left(1+\frac{1}{x}\right)\right]\div\frac{x-1}{x^3}\)
Tìm tập xác định
rút gọn biểu thức: A= (\(\left(\frac{1}{x-2}-\frac{2x}{4-x^2}+\frac{1}{2+x}\right).\left(\frac{2}{x}-1\right)\)
Tìm x : \(\frac{2\left(x-1\right)\left(x-3\right)}{3}-\frac{4\left(2x-1\right)^2}{5}=\frac{\left(1+3x\right)^2}{2}-3x\left(1-x\right)\)
Rút gọn:
a) P = \(\frac{bc}{\left(a-b\right)\left(a-c\right)}+\frac{ca}{\left(b-c\right)\left(b-a\right)}+\frac{ab}{\left(c-a\right)\left(c-b\right)}\)
b) Q = \(\frac{\left(x+\frac{1}{x}\right)^6-\left(x^6+\frac{1}{x^6}\right)-2}{\left(x+\frac{1}{x}\right)^3+x+\frac{1}{x^3}}\)
Giúp mik nhé!
cho biểu thức \(B=\left(\frac{21}{x^2-9}-\frac{x-4}{3-x}-\frac{x-1}{3+x}\right):\left(1-\frac{1}{x+3}\right)\)
a, rút gọn B
b,tính giá trị của biểu thức B tại x thỏa mãn \(\left|2x+1\right|=5\)
Giải các phương trình:a) frac{1}{x-1}-frac{3x^2}{x^3-1}frac{2x}{x^2+x+1}b) frac{3}{left(x-1right)left(x-2right)}+frac{2}{left(x-3right)left(x-1right)}frac{1}{left(x-2right)left(x-3right)}c) 1+frac{1}{x+2}frac{12}{8+x^3}d) frac{13}{left(x-3right)left(2x+7right)}+frac{1}{2x+7}frac{6}{left(x-3right)left(x+3right)}
Đọc tiếp
Giải các phương trình:
a) \(\frac{1}{x-1}-\frac{3x^2}{x^3-1}=\frac{2x}{x^2+x+1}\)
b) \(\frac{3}{\left(x-1\right)\left(x-2\right)}+\frac{2}{\left(x-3\right)\left(x-1\right)}=\frac{1}{\left(x-2\right)\left(x-3\right)}\)
c) \(1+\frac{1}{x+2}=\frac{12}{8+x^3}\)
d) \(\frac{13}{\left(x-3\right)\left(2x+7\right)}+\frac{1}{2x+7}=\frac{6}{\left(x-3\right)\left(x+3\right)}\)