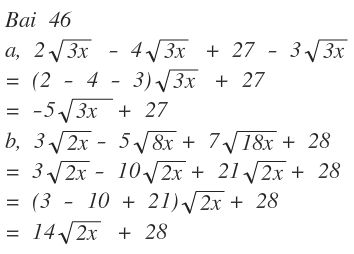Bài 6: Biến đối đơn giản biểu thức chứa căn bậc hai
Các câu hỏi tương tự
Rút gọn các biểu thức sau với \(x\ge0:\)
a. \(2\sqrt{3x}-4\sqrt{3x}+27-3\sqrt{3x};\)
b. \(3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+28.\)
rút gọn các biểu thức sau với x\(\ge\)0
a. \(2\sqrt{3}-4\sqrt{3x}+27-3\sqrt{3x}\)
b.\(3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+28\)
bài 1 : rút gọn các biểu thức sau .
a, sqrt[2]{3}-sqrt[4]{3x}+27-sqrt{27x}left(xge0right)
b,sqrt[3]{2x}-sqrt[5]{8x}+sqrt[7]{18x}+28
c, dfrac{2}{x^2-y^2}.sqrt{dfrac{3left(x+yright)^2}{2}}
d, dfrac{2}{2a-1}.sqrt{5a^2left(1-4a+4a^2right)}
bài 2 : biến đổi đơn giản
a, sqrt{7.6a^2.a^2}
b, sqrt{dfrac{4}{5}}
c, sqrt{dfrac{3}{2a^3}}(a0)
d,dfrac{7}{2sqrt{5}}
e, dfrac{10}{sqrt{3}+1}
f, dfrac{6}{sqrt{5}-sqrt{3}}
Đọc tiếp
bài 1 : rút gọn các biểu thức sau .
a, \(\sqrt[2]{3}-\sqrt[4]{3x}+27-\sqrt{27x}\left(x\ge0\right)\)
b,\(\sqrt[3]{2x}-\sqrt[5]{8x}+\sqrt[7]{18x}+28\)
c, \(\dfrac{2}{x^2-y^2}.\sqrt{\dfrac{3\left(x+y\right)^2}{2}}\)
d, \(\dfrac{2}{2a-1}.\sqrt{5a^2\left(1-4a+4a^2\right)}\)
bài 2 : biến đổi đơn giản
a, \(\sqrt{7.6a^2.a^2}\)
b, \(\sqrt{\dfrac{4}{5}}\)
c, \(\sqrt{\dfrac{3}{2a^3}}\)(a>0)
d,\(\dfrac{7}{2\sqrt{5}}\)
e, \(\dfrac{10}{\sqrt{3}+1}\)
f, \(\dfrac{6}{\sqrt{5}-\sqrt{3}}\)
Bài 1 : Giải pt
a) 2sqrt{2x} - 5sqrt{8x} + 7sqrt{18x} 28
b) sqrt{4x-20} + sqrt{x-5} - dfrac{1}{3}sqrt{9x-45} 4
c) sqrt{dfrac{3x-2}{x+1}} 2
d) dfrac{sqrt{5x-4}}{sqrt{x+2}} 2
Đọc tiếp
Bài 1 : Giải pt
a) 2\(\sqrt{2x}\) - 5\(\sqrt{8x}\) + 7\(\sqrt{18x}\) = 28
b) \(\sqrt{4x-20}\) + \(\sqrt{x-5}\) - \(\dfrac{1}{3}\)\(\sqrt{9x-45}\) = 4
c) \(\sqrt{\dfrac{3x-2}{x+1}}\) = 2
d) \(\dfrac{\sqrt{5x-4}}{\sqrt{x+2}}\) = 2
a chứng minh rằng: \(\dfrac{x+3+2.\sqrt{x^2-9}}{2x-6+\sqrt{x^2-9}}=\dfrac{\sqrt{x^2-9}}{x-3}\)
b rút gọn biểu thức T = \(\dfrac{x^2+5x+6+x.\sqrt{9-x^2}}{3x-x^2+\left(x+2\right)\sqrt{9-x^2}}\)
tính giá trị của biểu thức \(A=\left(3x^3+8x^2+2\right)^{2018}\)
với \(x=\dfrac{\left(\sqrt{5}+\sqrt{2}\right)\sqrt[3]{17\sqrt{5}-38}}{\sqrt{5}+\sqrt{14-6\sqrt{5}}}\)
giải các phương trình
a \(\sqrt{7+\sqrt{2x}=3+\sqrt{5}}\)
b \(\sqrt{3x^2-4x}=2x-3\)
c\(\dfrac{\left(7-x\right)\sqrt{7-x}+\left(x-5\right)\sqrt{x-5}}{\sqrt{7-x}+\sqrt{x-5}}=2\)
1) Giải các PT sau:
a)\(\sqrt{x+6-4\sqrt{x+2}}+\sqrt{x+11-6\sqrt{x+2}}=1\)
b)\(x^2-10x+27=\sqrt{6-x}+\sqrt{x-4}\)
c)\(x^2-2x-x\sqrt{x}-2\sqrt{x}+4=0\)
d)\(x^2+3x+1=\left(x+3\right)\sqrt{x^2+1}\)
e)\(2x+3=2\sqrt{x+1}+\sqrt{2x+1}\)
f)\(2+\sqrt{3-8x}=6x+\sqrt{4x-1}\)
Khai triển và rút gọn các biểu thức (với x, y không âm)
a) \(\left(4\sqrt{x}-\sqrt{2x}\right)\left(\sqrt{x}-\sqrt{2x}\right)\)
b) \(\left(2\sqrt{x}+\sqrt{y}\right)\left(3\sqrt{x}-2\sqrt{y}\right)\)