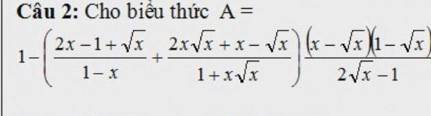Giải:
\(\sqrt{\left(\sqrt{x}-\sqrt{y}\right)^2\left(\sqrt{x}+\sqrt{y}\right)^2}\)
\(=\sqrt{\left[\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\right]\left[\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\right]}\)
\(=\sqrt{\left[\left(\sqrt{x}\right)^2-\left(\sqrt{y}\right)^2\right]\left[\left(\sqrt{x}\right)^2-\left(\sqrt{y}\right)^2\right]}\)
\(=\sqrt{\left(x-y\right)\left(x-y\right)}\left(y\ge x\ge0\right)\)
\(=\sqrt{\left(x-y\right)^2}\)
\(=\sqrt{\left(y-x\right)^2}\)
\(=y-x\left(y\ge x\right)\)
Vậy ...
Đúng 0
Bình luận (0)
