\(ĐK:a>0;a\ne1\\ A=\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}+\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}}\cdot\dfrac{a+2\sqrt{a}+1+a-2\sqrt{a}+1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ A=\dfrac{a+\sqrt{a}+1}{\sqrt{a}}-\dfrac{a-\sqrt{a}+1}{\sqrt{a}}+\dfrac{2a+2}{\sqrt{a}}\\ A=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1+2a+2}{\sqrt{a}}\\ A=\dfrac{2\left(a+\sqrt{a}+1\right)}{\sqrt{a}}=\dfrac{2\sqrt{a}\left(a+\sqrt{a}+1\right)}{a}\)
Ôn tập chương 1: Căn bậc hai. Căn bậc ba
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Rút gọn biểu thức: 
Rút gọn biểu thức: 
Rút gọn biểu thức: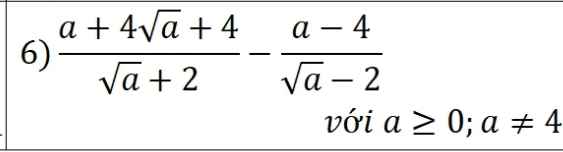
Rút gọn biểu thức sau
Đọc tiếp
Rút gọn biểu thức sau
Rút gọn các biểu thức sau
Đọc tiếp
Rút gọn các biểu thức sau
rút gọn biểu thức sau: \(\sqrt{5+\sqrt{21}}-\sqrt{5-\sqrt{21}}\)
rút gọn biểu thức sau: \(\sqrt{4+\sqrt{15}}-\sqrt{4-\sqrt{15}}\)
Rút gọn biểu thức sau:
(√12 - 2√18 + 5√3) x √3+5√6
Rút gọn biểu thức sau
a, \(\dfrac{53}{9-2\sqrt{7}}\) + 2√7 - 5








