\(\left(\sqrt{20}-\sqrt{45}+\sqrt{5}\right)\sqrt{5}\\ =\left(2\sqrt{5}-3\sqrt{5}+\sqrt{5}\right)\sqrt{5}\\ =\sqrt{5}\)
Đúng 0
Bình luận (0)
Bài 2: Căn thức bậc hai và hằng đẳng thức căn bậc hai của bình phương
Các câu hỏi tương tự
Rút gọn biểu thức sau;\(\sqrt{9-4}\sqrt{5}-\sqrt{5}\)
Bài 2 : Rút gọn biểu thức sau A = sqrt(5 - 2sqrt(6)) - sqrt((sqrt(2) - sqrt(3)) ^ 2)
Rút gọn căn thức: \(\sqrt{\sqrt{5}-\sqrt{5-\sqrt{21-4\sqrt{5}}}}\)
Rút gọn biểu thức:
h) \(\sqrt{\dfrac{3+\sqrt{5}}{\sqrt{3-\sqrt{5}}}}+\sqrt{\dfrac{3-\sqrt{5}}{\sqrt{3+\sqrt{5}}}}\)
Rút gọn biểu thức :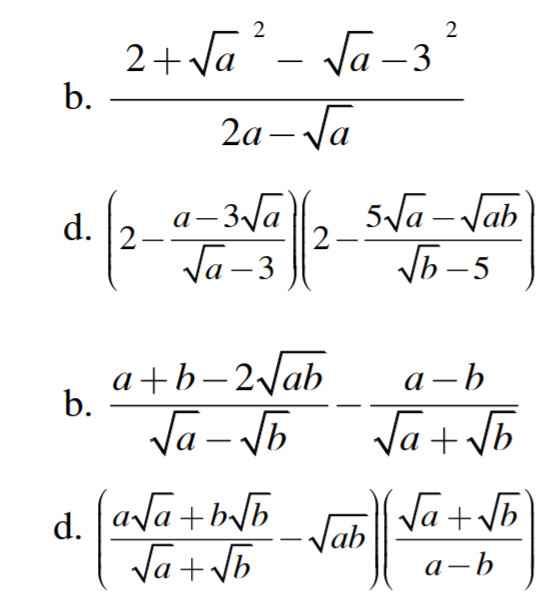
Rút gọn biểu thức: B=\(\sqrt{a+2\sqrt{a-1}}\)+\(\sqrt{a-2\sqrt{a-1}}\)
Cho biểu thức Q = A2 - B2
a) Rút gọn biểu thức
b) Tìm điều kiện của biểu thức
c) Tính giá trị của biểu thức
rút gọn biểu thức
căn(3-căn 3)^2
29 tháng 6 2021 lúc 18:19
2.4 Rút gọn biểu thức
\(a,\dfrac{3-\sqrt{x}}{x-9}\) ( vs x ≥ 0, x≠ 9)
b, \(\dfrac{x-5\sqrt{x}+6}{\sqrt{x}-3}\)( vs x ≥ 0 ; x ≠ 9)
c, \(6-2x-\sqrt{9-6x+x^2}\left(x< 3\right)\)