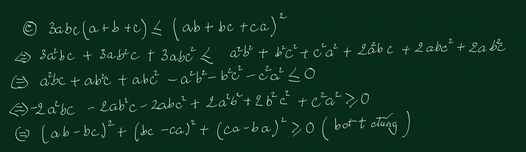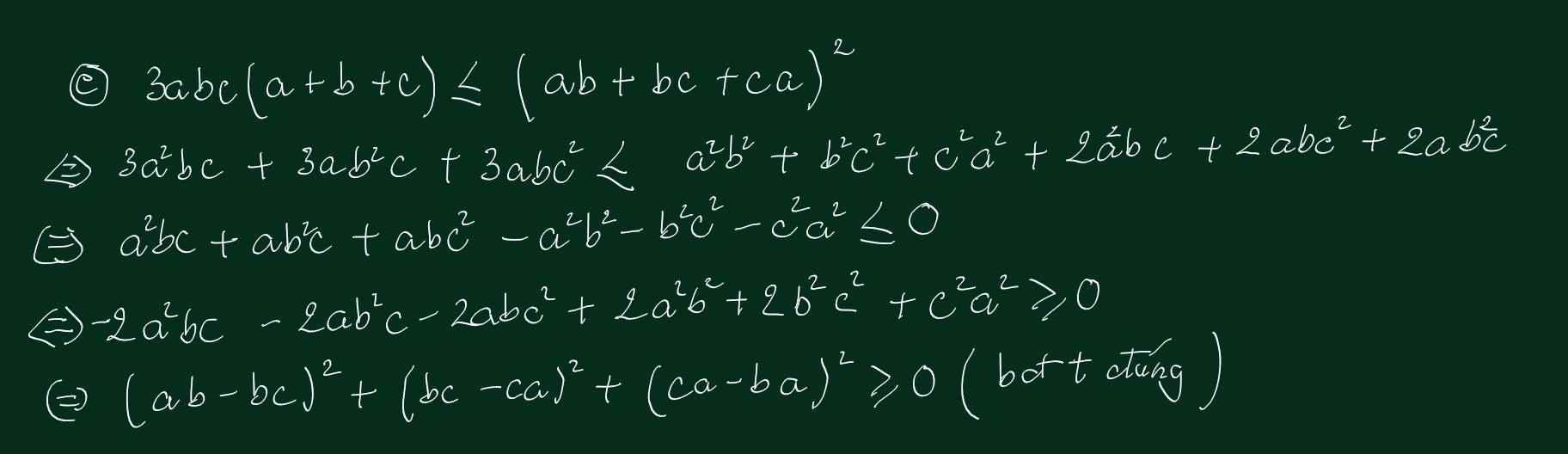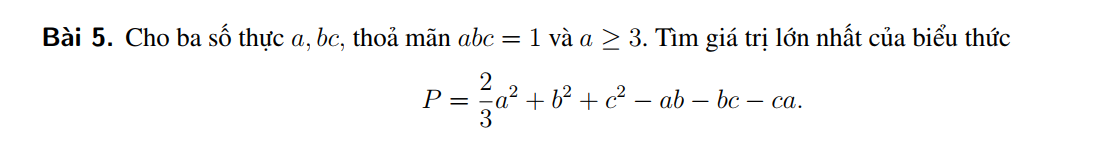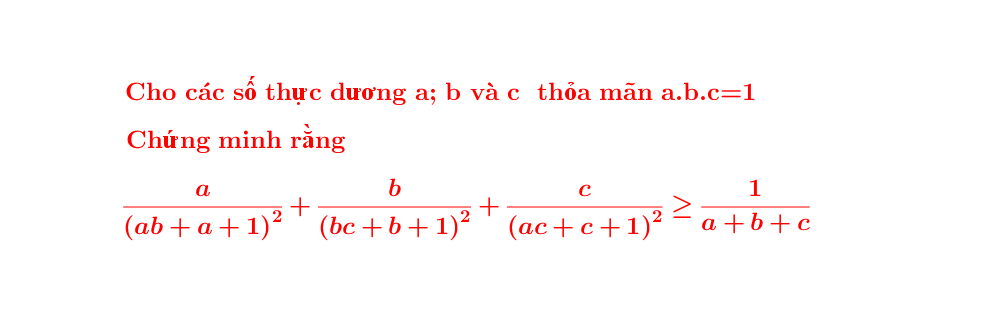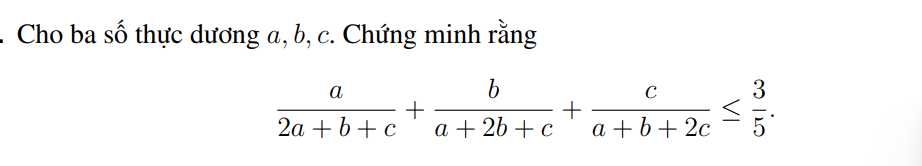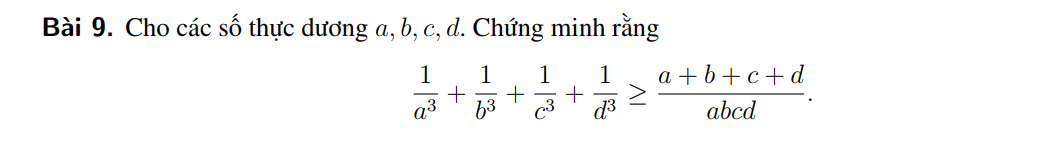Hai câu c và d chỉ là BĐT \(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\), cách chứng minh \(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\) thế nào thì chứng minh c và d như vậy (biến đổi thành tổng của 3 bình phương các hiệu)
Với câu c thì \(x=ab;y=bc;z=ca\), câu d thì \(x=a^2b;y=...\)
Với mọi a;b;c ta luôn có:
\(\left(a^2b-b^2c\right)^2+\left(a^2b-c^2a\right)^2+\left(b^2c-c^2a\right)\ge0\)
\(\Leftrightarrow a^4b^2+b^4c^2+c^4a^2\ge a^2b^3c+a^3bc^2+ab^2c^3\)
\(\Leftrightarrow a^4b^2+b^4c^2+c^4a^2+2\left(a^2b^3c+a^3bc^2+ab^2c^3\right)\ge3\left(a^2b^3c+a^3bc^2+ab^2c^3\right)\)
\(\Leftrightarrow\left(a^2b+b^2c+c^2a\right)^2\ge3\left(a^2b^3c+a^3bc^2+ab^2c^3\right)=3abc\left(ab^2+bc^2+ca^2\right)\)