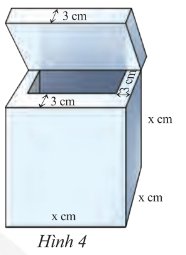
Sức chứa của thùng: `(x-3.2)^3 = (x-6)^3 = x^3 - 18x^2 + 108x - 216(cm^3)`.
Bài 3. Hằng đẳng thức đáng nhớ
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
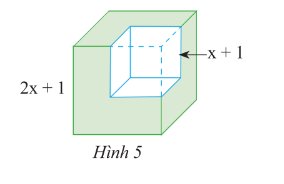
Từ một khối lập phương có cạnh bằng \(2x + 1\), ta cắt bỏ một khối lập phương có cạnh bằng \(x + 1\) (xem Hình 5). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.
a) Viết biểu thức tính diện tích của hình vuông có cạnh bằng 2x+3dưới dạng đa thức
b) Viết biểu thức tính thể tích của khối lập phương có cạnh bằng 3x−2dưới dạng đa thức.
a) Một mảnh vườn hình vuông có cạnh 10m được mở rộng cả hai cạnh thêm x (m) như Hình 2a. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn sau khi mở rộng.b) Một mảnh vườn hình vuông sau khi mở rộng mỗi cạnh 5m thì được một mảnh vườn hình vuông có cạnh là x (m) như Hình 2b. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn trước khi mở rộng.
Đọc tiếp
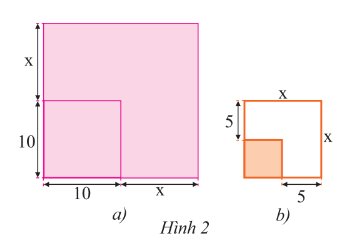
a) Một mảnh vườn hình vuông có cạnh \(10\)m được mở rộng cả hai cạnh thêm \(x\) (m) như Hình 2a. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn sau khi mở rộng.
b) Một mảnh vườn hình vuông sau khi mở rộng mỗi cạnh \(5\)m thì được một mảnh vườn hình vuông có cạnh là \(x\) (m) như Hình 2b. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn trước khi mở rộng.
a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích S của các phần tô màu trong Hình 1 như sau:Kết quả của mỗi bạn có đúng không? Giải thích.b) Thực hiện phép nhân và rút gọn đa thức của bạn An.c) Bằng cách làm tương tự ở câu b), có thể biến đổi biểu thức {left( {a - b} right)^2} thành biểu thức nào?
Đọc tiếp
a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích \(S\) của các phần tô màu trong Hình 1 như sau:

Kết quả của mỗi bạn có đúng không? Giải thích.
b) Thực hiện phép nhân và rút gọn đa thức của bạn An.
c) Bằng cách làm tương tự ở câu b), có thể biến đổi biểu thức \({\left( {a - b} \right)^2}\) thành biểu thức nào?
Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng \(5\)cm. Thể tích của hình hộp chữ nhật sẽ tăng bao nhiêu nếu:
a) Chiều dài và chiều rộng tăng thêm \(a\) cm?
b) Chiều dài, chiều rộng, chiều cao đều tăng thêm \(a\) cm?
Viết các đa thức sau dưới dạng tích:
a) \(8{y^3} + 1\) b) \({y^3} - 8\)
a) Từ Hình 3a, người ta cắt ghép tạo thành Hình 3b. Viết hai biểu thức khác nhau, mỗi biểu thức biểu thị diện tích (phần tô màu) của một trong hai hình bên.b) Thực hiện phép nhân và rút gọn đa thức, biến đổi biểu thức left( {a + b} right)left( {a - b} right) thành một đa thức thu gọn. Từ đó, có kết luận gì về diện tích của hai hình bên?
Đọc tiếp
a) Từ Hình 3a, người ta cắt ghép tạo thành Hình 3b. Viết hai biểu thức khác nhau, mỗi biểu thức biểu thị diện tích (phần tô màu) của một trong hai hình bên.
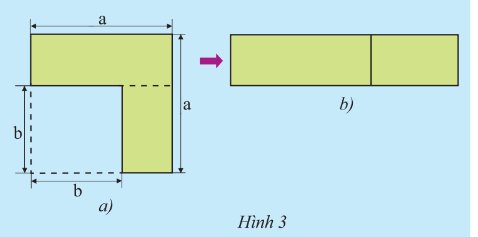
b) Thực hiện phép nhân và rút gọn đa thức, biến đổi biểu thức \(\left( {a + b} \right)\left( {a - b} \right)\) thành một đa thức thu gọn. Từ đó, có kết luận gì về diện tích của hai hình bên?
Hoàn thành các phép nhân đa thức sau vào vở, thu gọn kết quả nhận được:begin{array}{l}{left( {a + b} right)^3} left( {a + b} right){left( {a + b} right)^2};;;;;;;;;;; left( {a + b} right)left( {...} right);;;;;;;;;;; ...end{array} begin{array}{l}{left( {a - b} right)^3} left( {a - b} right){left( {a - b} right)^2};;;;;;;;;;; left( {a - b} right)left( {...} right);;;;;;;;;;; ...end{array}
Đọc tiếp
Hoàn thành các phép nhân đa thức sau vào vở, thu gọn kết quả nhận được:
\(\begin{array}{l}{\left( {a + b} \right)^3} = \left( {a + b} \right){\left( {a + b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\;\; = ...\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = \left( {a - b} \right){\left( {a - b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\;\; = ...\end{array}\)
Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:
a) \({x^2} + 2x + 1\) b) \(9 - 24x + 16{x^2}\) c) \(4{x^2} + \dfrac{1}{4} + 2x\)