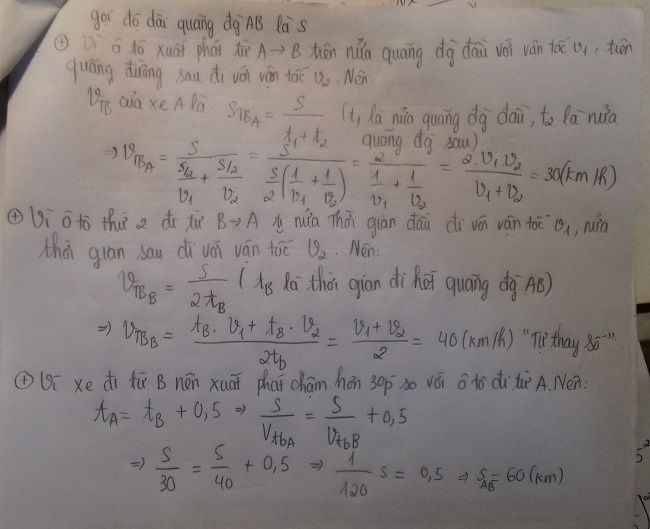Một ô tô xuất phát từ A đi đến đích B , trên nửa quãng đường đầu đi với vận tốc v1 và trên nửa quãng đường sau đi với vận tốc v2 . Một ô tô thứ hai xuất phát từ B đến đích A , trong nửa thời gian đầu đi với vận tốc v1 và trong nửa thời gian sau đi với vận tốc v2. Biết v1=20km/h , v2=60km/h. Nếu xe đi từ B xuất phát muộn hơn xe đi A là 30 phút thì 2 xe tới đích cùng lúc . Tính chiều dài quãng đường AB. nếu hai xe xuất phát cung lúc thì chúng sẽ gạp nhau tai vị trí cách A một khoảng bao nhiêu
Thời gian đi của ô tô thứ nhất:
\(t_1=\dfrac{s}{2v_1}+\dfrac{s}{2v_2}=\dfrac{s\left(v_1+v_2\right)}{2v_1v_2}\)
Vận tốc trung bình của ô tô thứ nhất:
\(v_{tbA}=\dfrac{s}{t}=\dfrac{2v_1v_2}{v_1+v_2}=\dfrac{2.20.60}{20+60}=30km/h\)
Theo đề ta có: \(s=\dfrac{t_2}{2}v_1+\dfrac{t_2}{2}v_2=t_2\left(\dfrac{v_1+v_2}{2}\right)\)
Vận tốc trung bình của ô tô thứ hai:
\(v_{tbB}=\dfrac{s}{t_2}=\dfrac{v_1+v_2}{2}=\dfrac{20+60}{2}=40km/h\)
Theo đề bài ta có: \(\dfrac{s}{v_A}-\dfrac{s}{v_B}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{s}{30}-\dfrac{s}{40}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{4s}{120}-\dfrac{3s}{120}=\dfrac{60}{120}\)
\(\Leftrightarrow s=60\left(km\right)\)
Vậy hai xe xuất phát cùng lúc sẽ gặp nhau sau:
\(s_1+s_2=s_{AB}\)
\(\Leftrightarrow30t+40t=60\)
\(\Leftrightarrow70t=60\)
\(\Leftrightarrow t=\dfrac{60}{70}\approx0,9\left(h\right)\)
Hai xe gặp nhau tại điểm cách điểm A:
\(s_1=v_A.t=30.0,9=27\left(km\right)\)
hời gian đi của ô tô thứ nhất:
vtbA=st=2v1v2v1+v2=2.20.6020+60=30km/h����=��=2�1�2�1+�2=2.20.6020+60=30��/ℎ
Theo đề ta có: vtbB=st2=v1+v22=20+602=40km/h����=��2=�1+�22=20+602=40��/ℎ
Theo đề bài ta có: ⇔s30−s40=12⇔�30−�40=12
⇔t=6070≈0,9(h)⇔�=6070≈0,9(ℎ)
Hai xe gặp nhau tại điểm cách điểm A:
s1=vA.t=30.0,9=27(km)�1=��.�=30.0,9=27(��)