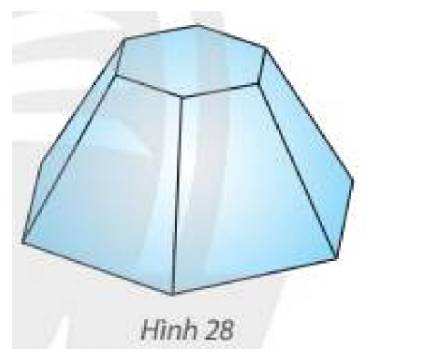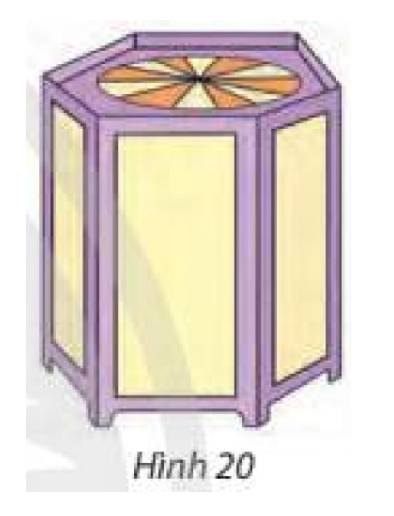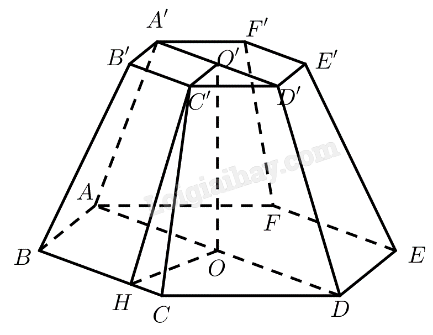
Mô hình hoá hình ảnh cái bục bằng hình chóp cụt lục giác đều \(ABC{\rm{DEF}}{\rm{.}}A'B'C'{\rm{D'E'F'}}\) có \(O\) và \(O'\) là tâm của hai đáy. Kẻ \(C'H \bot BC\left( {H \in BC} \right)\).
Ta có: \(BC = 1;CC' = B'C' = 0,7\).
Diện tích đáy lớn là: \(6.\frac{{B{C^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{2}\)
Diện tích đáy nhỏ là: \(6.\frac{{B'C{'^2}\sqrt 3 }}{4} = \frac{{147\sqrt 3 }}{{200}}\)
\(BCC'B'\) là hình thang cân nên \(HC = \frac{{BC - B'C'}}{2} = 0,15\)
Tam giác \(CC'H\) vuông tại \(H \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}} = \frac{{\sqrt {187} }}{{20}}\)
Diện tích một mặt bên là: \(\frac{1}{2}\left( {BC + B'C'} \right).C'H = \frac{{17\sqrt {187} }}{{400}}\)
Diện tích sáu mặt bên là: \(6.\frac{{17\sqrt {187} }}{{400}} = \frac{{51\sqrt {187} }}{{200}}\)
Diện tích cần sơn là: \(\frac{{51\sqrt {187} }}{{200}} + \frac{{3\sqrt 3 }}{2} + \frac{{147\sqrt 3 }}{{200}} \approx 7,36\left( {{m^2}} \right)\)