khi đó diện tích xung quanh bằng diện tích của hình chữ nhật có chiều dài bằng chu vi đáy có bán kính 3cm và chiều rộng bằng 5cm
Ôn tập chương Hình trụ, Hình nón, Hình cầu
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Một hình chữ nhật ABCD có AB > AD, diện tích và chu vi của nó theo thứ tự là 2a2 và 6a. Cho hình vẽ quay xung quanh cạnh AB, ta được một hình trụ.
Tính diện tích xung quanh và thể tích của hình trụ này.
Một hình chữ nhật có chiều dài gấp hai lần chiều rộng, quay hình chữ nhật đó một vòng quanh chiều dài cố định ta được một hình trụ có diện tích xung quanh bằng 100π cm2 Tính bán kính đáy r và chiều cao h của hình trụ.
Một hình trụ được "đặt khít" vào bên trong một hình cầu bán kính \(r=12cm\), như hình 112.
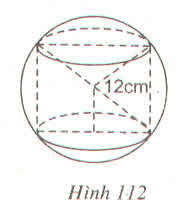
Hãy tính :
a) Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ bằng đường kính đáy của nó
b) Thể tích hình cầu
c) Diện tích mặt cầu
Với nửa hình cầu bán kính r và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng h
a) Khi r = 12 (cm) và thể tích hai hình bằng nhau thì giá trị h(cm) làm tròn đến chữ số thập phân thứ nhất là bao nhiêu ?
b) Khi h = 12 (cm) và tổng diện tích nửa mặt cầu và diện tích "hình tròn đáy" gấp ba lần diện tích toàn phần của hình trụ thì r (cm) bằng bao nhiêu ?
Một hình nón có bán kính đáy bằng và diện tích xung quanh bằng. Tính thể tích khối nón?
cho hình vuông ABCD có cạnh AD=3a với a<0, a thuộc R. Tính theo a diện tích xung quanh và thể tích của hình trụ tạo bởi hình vuông ABCD quay quanh đường thẳng MN
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h. 119). Cho hình đó quay xung quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
Đọc tiếp
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h. 119). Cho hình đó quay xung quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
-0132.jpg)
giải hộ mình 2 bài này với mình cảm ơn nhiều
Bài1: Một hình thang ABCD có góc A và góc D bằng 90 độ, ABBCa, góc C60 độ. Tính diện tích của hình tạo thành khi quay hình thang vuông một vòng xung quanh cạnh AD
Bài 2: Một hình trụ có bán kính r và chiều cao hr căn 3
a)Tính diện tích xung quanh, diện tích toàn phần của hình trụ
b)Tính thể tích khối trụ tạo nên bởi hình trụ đã cho.
Đọc tiếp
giải hộ mình 2 bài này với mình cảm ơn nhiều
Bài1: Một hình thang ABCD có góc A và góc D bằng 90 độ, AB=BC=a, góc C=60 độ. Tính diện tích của hình tạo thành khi quay hình thang vuông một vòng xung quanh cạnh AD
Bài 2: Một hình trụ có bán kính r và chiều cao h=r căn 3
a)Tính diện tích xung quanh, diện tích toàn phần của hình trụ
b)Tính thể tích khối trụ tạo nên bởi hình trụ đã cho.
Độ dài các cạnh của một tam giác ABC vuông tại A, thỏa mãn các hệ thức sau :
BCAB+2a
ACdfrac{1}{2}left(BC+ABright)
a là một độ dài cho trước
a) Tính theo a, độ dài các cạnh và chiều cao AH của tam giác
b) Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác ssos
c) Cho tam giác ABC quay một vòng quanh cạnh huyền BC. Tính tỉ số diện tích giữa các phần do các dây cung AB và...
Đọc tiếp
Độ dài các cạnh của một tam giác ABC vuông tại A, thỏa mãn các hệ thức sau :
\(BC=AB+2a\)
\(AC=\dfrac{1}{2}\left(BC+AB\right)\)
a là một độ dài cho trước
a) Tính theo a, độ dài các cạnh và chiều cao AH của tam giác
b) Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác ssos
c) Cho tam giác ABC quay một vòng quanh cạnh huyền BC. Tính tỉ số diện tích giữa các phần do các dây cung AB và AC tạo ra








