Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)
Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8 m, rộng 20 m (hình 16)
a) Chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên
b) Tính khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm

Viết phương trình chính tắc của elip trong hình 4.

Viết phương trình chính tắc của:
a) Elip có trục lớn bằng 20 và trục nhỏ bằng 16
b) Hypebol có tiêu cự \(2c = 20\) và độ dài trục thực \(2a = 12\)
c) Parabol có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\)
Để cắt một bảng hiệu quảng cáo hình Elip có trục lớn là 80 cm và trục nhỏ là 40 cm từ một tấm ván ép hình chữ nhật có kích thước là 80 cm x 40 cm, người ta vẽ hình elip đó trên tấm ván ép như hướng dẫn sau:
Chuẩn bị
- Hai cái đinh, một vòng dây kín không đàn hồi, bút chì.
Thực hiện
- Xác định vị trí (hai tiêu điểm của elip) và ghim hai cái đinh trên 2 điểm đó trên tấm ván.
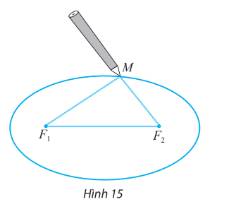
- Quàng vòng dây qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một đường elip (Xem minh họa trong hình 15).
Phải ghim hai cái đinh cách các mép tấm bìa bao nhiêu xentimets và lấy vòng dây có độ dài là bao nhiêu?
Viết phương trình chính tắc của parabol (P) có đường chuẩn \(\Delta :x + 1 = 0\)
Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m.
Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục nhỏ bằng 6.
Một tháp làm nguội của một nhà máy có mặt cắt là hình hyperbol có phương trình \(\frac{{{x^2}}}{{{{28}^2}}} - \frac{{{y^2}}}{{{{42}^2}}} = 1\) (hình 17). Biết chiều cao của tháp là 150 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol là \(\frac{2}{3}\) khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính đáy của tháp.

Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm tọa độ của các tiêu điểm của chúng
a) \(({C_1}):4{x^2} + 16{y^2} = 1\)
b) \(({C_2}):16{x^2} - 4{y^2} = 144\)
c) \(({C_3}):x = \frac{1}{8}{y^2}\)