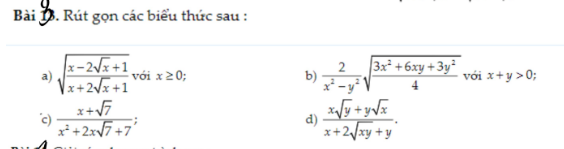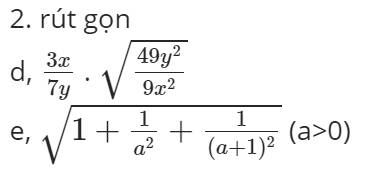\(a.\sqrt{\dfrac{x-2\sqrt{x}+1}{x+2\sqrt{x}+1}=\sqrt{\dfrac{\left(\sqrt{x}-1\right)^{^2}}{\left(\sqrt{x+1}\right)^{^2}}}}=\dfrac{\left|\sqrt{x}-1\right|}{\left|\sqrt{x}+1\right|}\)
a: \(=\sqrt{\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)^2}}=\dfrac{\left|\sqrt{x}-1\right|}{\sqrt{x}+1}\)
b: \(=\dfrac{2}{\left(x-y\right)\left(x+y\right)}\cdot\dfrac{\sqrt{3}\left(x+y\right)}{2}=\dfrac{\sqrt{3}}{x-y}\)
c: \(=\dfrac{x+\sqrt{7}}{\left(x+\sqrt{7}\right)^2}=\dfrac{1}{x+\sqrt{7}}\)
`a,sqrt((x-2 sqrt x+1)/(x+2sqrt x +1)`
` = sqrt((sqrt x-1)/(sqrt x+1)^2)`
`= (sqrt x- 1)/(sqrt x +1)`.
`b, = 2/((x-y)(x+y)) . ( sqrt. 3(x+y))/2`
`= sqrt 3/(x-y)`
`c, = (x+sqrt 7)/(x + sqrt 7)^2`
`= 1/(x + sqrt 7)^2`
`d, = (sqrt (xy) . (sqrt x + sqrt y))/(sqrt x + sqrt y)^2`
`= (sqrt(xy))/(sqrt x + sqrt y)`