A = \(4\sqrt{20}+2\sqrt{45}-8\sqrt{5}+2\sqrt{180}\)
A = \(4.2\sqrt{5}+2.3\sqrt{5}-8\sqrt{5}+2.6\sqrt{5}\)
A = \(8\sqrt{5}+6\sqrt{5}-8\sqrt{5}+12\sqrt{5}\)
A = \(\left(8+6-8+12\right)\sqrt{5}\)
A = \(6\sqrt{5}\)
\(A=4\sqrt{20}+2\sqrt{45}-8\sqrt{5}+2\sqrt{180}\)
\(=8\sqrt{5}+6\sqrt{5}-8\sqrt{5}+12\sqrt{5}\)
\(=18\sqrt{5}\)
\(B=\dfrac{1}{\sqrt{5}+\sqrt{7}}-\dfrac{1}{\sqrt{5}-\sqrt{7}}\)
\(=\dfrac{\sqrt{5}-\sqrt{7}-\sqrt{5}-\sqrt{7}}{\left(\sqrt{5}+\sqrt{7}\right)\left(\sqrt{5}-\sqrt{7}\right)}\)
\(=\dfrac{-2\sqrt{7}}{2}\)
\(=-\sqrt{7}\)
Bài 2:
\(\sqrt{xy}+1+\sqrt{x}+\sqrt{y}\)
\(=\sqrt{x}\left(\sqrt{y}+1\right)+\sqrt{y}+1\)
\(=\left(\sqrt{x}+1\right)\left(\sqrt{y}+1\right)\)
Bài 1:
A= \(4\sqrt{20}+2\sqrt{45}-8\sqrt{5}+2\sqrt{180}\)
= \(4\sqrt{4.5}+2\sqrt{9.5}-8\sqrt{5}+2\sqrt{36.5}\)
= \(8\sqrt{5}+6\sqrt{5}-8\sqrt{5}+12\sqrt{5}\)
= \(\left(8+6-8+12\right)\sqrt{5}\)
= \(18\sqrt{5}\)
B= \(\dfrac{1}{\sqrt{5}+\sqrt{7}}-\dfrac{1}{\sqrt{5}-\sqrt{7}}\)
= \(\dfrac{\left(\sqrt{5}-\sqrt{7}\right)-\left(\sqrt{5}+\sqrt{7}\right)}{\left(\sqrt{5}+\sqrt{7}\right)\left(\sqrt{5}-\sqrt{7}\right)}\)
= \(\dfrac{\sqrt{5}-\sqrt{7}-\sqrt{5}-\sqrt{7}}{\sqrt{5^2}-\sqrt{7^2}}\)
= \(\dfrac{-2\sqrt{7}}{5-7}\)
= \(\dfrac{-2\sqrt{7}}{-2}\)
= \(\sqrt{7}\)
C= \(\sqrt{\dfrac{4+\sqrt{7}}{4-\sqrt{7}}}+\sqrt{\dfrac{4-\sqrt{7}}{4+\sqrt{7}}}\)
= \(\sqrt{\dfrac{\left(4+\sqrt{7}\right)^2}{\left(4-\sqrt{7}\right)\left(4+\sqrt{7}\right)}}+\sqrt{\dfrac{\left(4-\sqrt{7}\right)^2}{\left(4+\sqrt{7}\right)\left(4-\sqrt{7}\right)}}\)
= \(\sqrt{\dfrac{\left(4+\sqrt{7}\right)^2}{4^2-\sqrt{7^2}}}+\sqrt{\dfrac{\left(4-\sqrt{7}\right)^2}{4^2-\sqrt{7^2}}}\)
= \(\sqrt{\dfrac{\left(4+\sqrt{7}\right)^2}{9}}+\sqrt{\dfrac{\left(4-\sqrt{7}\right)^2}{9}}\)
= \(\dfrac{\sqrt{\left(4+\sqrt{7}\right)^2}}{\sqrt{9}}+\dfrac{\sqrt{\left(4-\sqrt{7}\right)^2}}{\sqrt{9}}\)
= \(\dfrac{\left|4+\sqrt{7}\right|}{3}+\dfrac{\left|4-\sqrt{7}\right|}{3}\)
= \(\dfrac{\left(4+\sqrt{7}\right)+\left(4-\sqrt{7}\right)}{3}\)
= \(\dfrac{8}{3}\)
D= \(\sqrt{5+\sqrt{21}}+\sqrt{5-\sqrt{21}}\)
\(\Rightarrow D^2=\left(\sqrt{5+\sqrt{21}}+\sqrt{5-\sqrt{21}}\right)^2\)
= \(\left(\sqrt{5+\sqrt{21}}\right)^2+2.\sqrt{5+\sqrt{21}}.\sqrt{5-\sqrt{21}}+\left(\sqrt{5-\sqrt{21}}\right)^2\)
= \(\left|5+\sqrt{21}\right|+2\sqrt{\left(5+\sqrt{21}\right)\left(5-\sqrt{21}\right)}+\left|5-\sqrt{21}\right|\)
= \(5+\sqrt{21}+2\sqrt{25-21}+5-\sqrt{21}\)
= \(10+2\sqrt{4}\)
= 10+4=14
Bài 2:
\(\sqrt{xy}+1+\sqrt{x}+\sqrt{y}\)
= \(\left(\sqrt{xy}+\sqrt{x}\right)+\left(\sqrt{y}+1\right)\)
= \(\sqrt{x}\left(\sqrt{y}+1\right)+\left(\sqrt{y}+1\right)\)
= \(\left(\sqrt{y}+1\right)\left(\sqrt{x}+1\right)\)
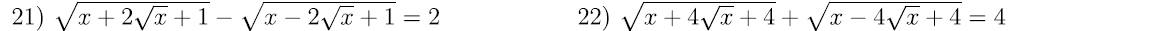Mọi người giúp em với ạ
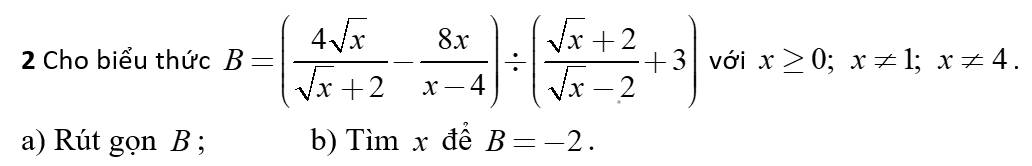mọi người giúp em với ạ
