3.
a. Mỗi vị trí có 8 cách chọn, do đó có thể lập \(3^8\) chữ số
b. Số số thỏa mãn: \(8.7.6=...\)
c. Chữ số hàng đơn vị phải là số chẵn \(\Rightarrow\) có 4 cách chọn
Hai chữ số còn lại có \(7.6\) cách
Tổng: \(4.7.6=...\)
d. Chia X làm 3 tập: \(A=\left\{3;6\right\}\) gồm các chữ số chia hết cho 3
\(B=\left\{1;4;7\right\}\) gồm các số chia 3 dư 1
\(C=\left\{2;5;8\right\}\) gồm các số chia 3 dư 2
Số được lập thỏa mãn khi các TH sau xảy ra: (3 số được chọn nằm cùng 1 tập), (3 số được chọn nằm ở 3 tập khác nhau)
\(\Rightarrow3!+3!+3!.C_2^1.C_3^1.C_3^1=...\)
4.
Gọi chữ số cần lập là \(\overline{abc}\)
a.
a có 6 cách chọn, b và c mỗi vị trí có 7 cách chọn
\(\Rightarrow6.7.7=...\) số
b.
a có 6 cách chọn (khác 0), b có 6 cách chọn (khác a), c có 5 cách chọn (khác a và b)
\(\Rightarrow6.6.5=...\) số
c.
- Nếu \(c=0\Rightarrow\) a có 6 cách chọn, b có 5 cách chọn \(\Rightarrow6.5\) số
- Nếu \(c\ne0\Rightarrow c\) có 3 cách chọn (2;4;6), a có 5 cách chọn (khác c và 0), b có 5 cách chọn (khác a và c) \(\Rightarrow3.5.5\) số
Tổng cộng: \(6.5+3.5.5=...\) số
4.
d.
Chia X làm 3 tập: \(A=\left\{0;3;6\right\}\) ; \(B=\left\{1;4\right\}\) ; \(C=\left\{2;5\right\}\)
Số được lập sẽ chia hết cho 3 khi: (3 chữ số cùng thuộc 1 tập), (3 chữ số nằm ở 3 tập khác nhau)
Th1: 3 chữ số cùng thuộc 1 tập thì chúng chỉ có thể cùng thuộc A (vì B và C ít hơn 3 phần tử)
Số số thỏa mãn: \(3!-2!=4\)
TH2: 3 chữ số thuộc 3 tập khác nhau:
- Nếu số được chọn từ A là 0 \(\Rightarrow\) có 1 cách chọn, từ B và C đều có \(C_2^1\) cách
\(\Rightarrow\) Có \(1.C_2^1.C_2^1=...\) bộ
Hoán vị chúng và loại trừ trường hợp 0 đứng đầu: \(\left(3!-2!\right).1.C_2^1.C_2^1=16\)
- Nếu số được chọn từ A không phải số 0 \(\Rightarrow\) có 2 cách, chọn 1 số từ B và C vẫn có \(C_2^1.C_2^1=4\) cách
\(\Rightarrow\) Có \(2.4=8\) bộ
Hoán vị chúng: \(3!.8=48\) số
Vậy có tổng cộng: \(4+16+48=...\) số
4.
e.
- Nếu \(c=0\Rightarrow\) a và b lần lượt có 6 và 5 cách chọn \(\Rightarrow6.5\) số
- Nếu \(c=5\Rightarrow a\) có 5 cách chọn (khác c và 0), b có 5 cách chọn (khác a và c) \(\Rightarrow5.5\) số
Tổng tộng: \(6.5+5.5=...\)
f.
- Nếu \(a\ge4\Rightarrow a\) có 3 cách chọn (4;5;6)
Khi đó ta có thể chọn b, c tùy ý thì vẫn luôn thỏa mãn \(\overline{abc}\ge356\)
b có 6 cách chọn (khác a), c có 5 cách chọn (khác a và b)
\(\Rightarrow3.6.5\) số
- Nếu \(a=3\Rightarrow b\ge5\)
+ Nếu \(b=5\Rightarrow c=6\) có 1 cách chọn
+ Nếu \(b=6\Rightarrow\) c có thể chọn tùy ý mà vẫn thỏa mãn \(\Rightarrow c\) có 5 cách chọn (khác a và b)
\(\Rightarrow1+5=6\) số
Vậy có tổng cộng: \(3.6.5+6=...\)












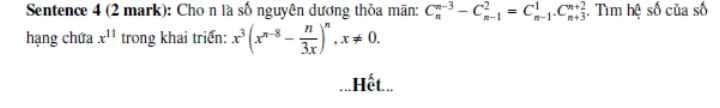





 giúp mình với ạ
giúp mình với ạ