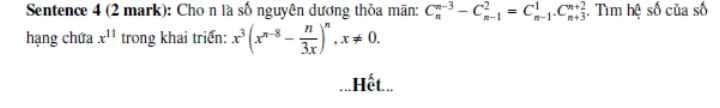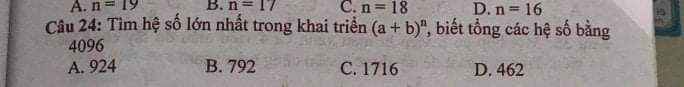Điều kiện: \(n\ge3\)
Giả thiết tương đương:
\(\dfrac{n!}{\left(n-3\right)!.3!}-\dfrac{\left(n-1\right)!}{2!\left(n-3\right)!}=\dfrac{\left(n-1\right)!}{\left(n-2\right)!}.\dfrac{\left(n+3\right)!}{\left(n+2\right)!}\)
\(\Leftrightarrow\dfrac{n\left(n-1\right)\left(n-2\right)}{6}-\dfrac{\left(n-1\right)\left(n-2\right)}{2}=\left(n-1\right)\left(n+3\right)\)
\(\Leftrightarrow\dfrac{n\left(n-2\right)}{6}-\dfrac{n-2}{2}=n+3\)
\(\Leftrightarrow n^2-11n-12=0\Rightarrow\left[{}\begin{matrix}n=12\\n=-1\left(loại\right)\end{matrix}\right.\)
Vậy khai triển đã cho là: \(x^3\left(x^3-\dfrac{12}{3x}\right)^{12}=x^3\left(x^3-\dfrac{4}{x}\right)^{12}\)
Số hạng tổng quát trong khai triển:
\(C_{12}^k.\left(x^3\right)^k.\left(-\dfrac{4}{x}\right)^{12-k}.x^3=C_{12}^k.\left(-4\right)^{12-k}.x^{4k-9}\)
Số hạng chứa \(x^{11}\) thỏa mãn:
\(4k-9=11\Leftrightarrow k=5\)
Hệ số: \(C_{12}^5.\left(-4\right)^7=-C_{12}^5.4^7=...\)