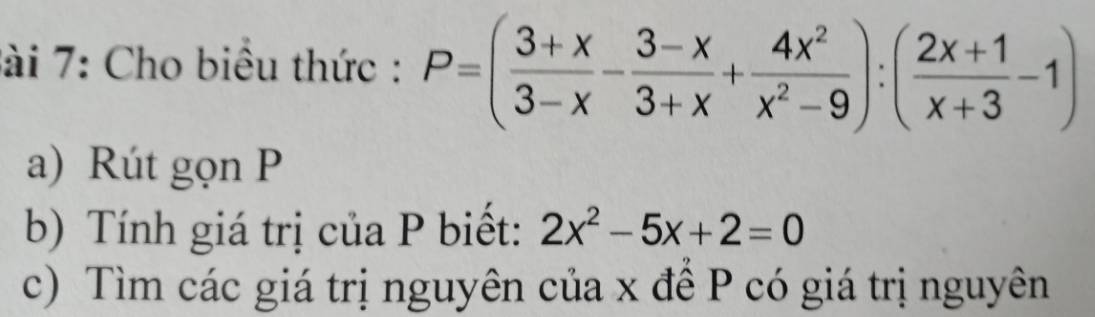a: \(P=\left(\dfrac{-\left(x+3\right)}{x-3}+\dfrac{x-3}{x+3}+\dfrac{4x^2}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{2x+1-x-3}{x+3}\)
\(=\dfrac{-x^2-6x-9+x^2-6x+9+4x^2}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x-2}\)
\(=\dfrac{4x^2-12x}{\left(x-3\right)}\cdot\dfrac{1}{x-2}=\dfrac{4x}{x-2}\)
b: 2x^2-5x+2=0
=>2x^2-4x-x+2=0
=>(x-2)(2x-1)=0
=>x=1/2(nhận) hoặc x=2(loại)
Khi x=1/2 thì \(P=\dfrac{4\cdot\dfrac{1}{2}}{\dfrac{1}{2}-2}=2:\dfrac{-3}{2}=-\dfrac{4}{3}\)
c: ĐểP nguyên thì 4x-8+8 chia hết cho x-2
=>\(x-2\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
=>\(x\in\left\{1;4;0;6;-2;10;-6\right\}\)