4.
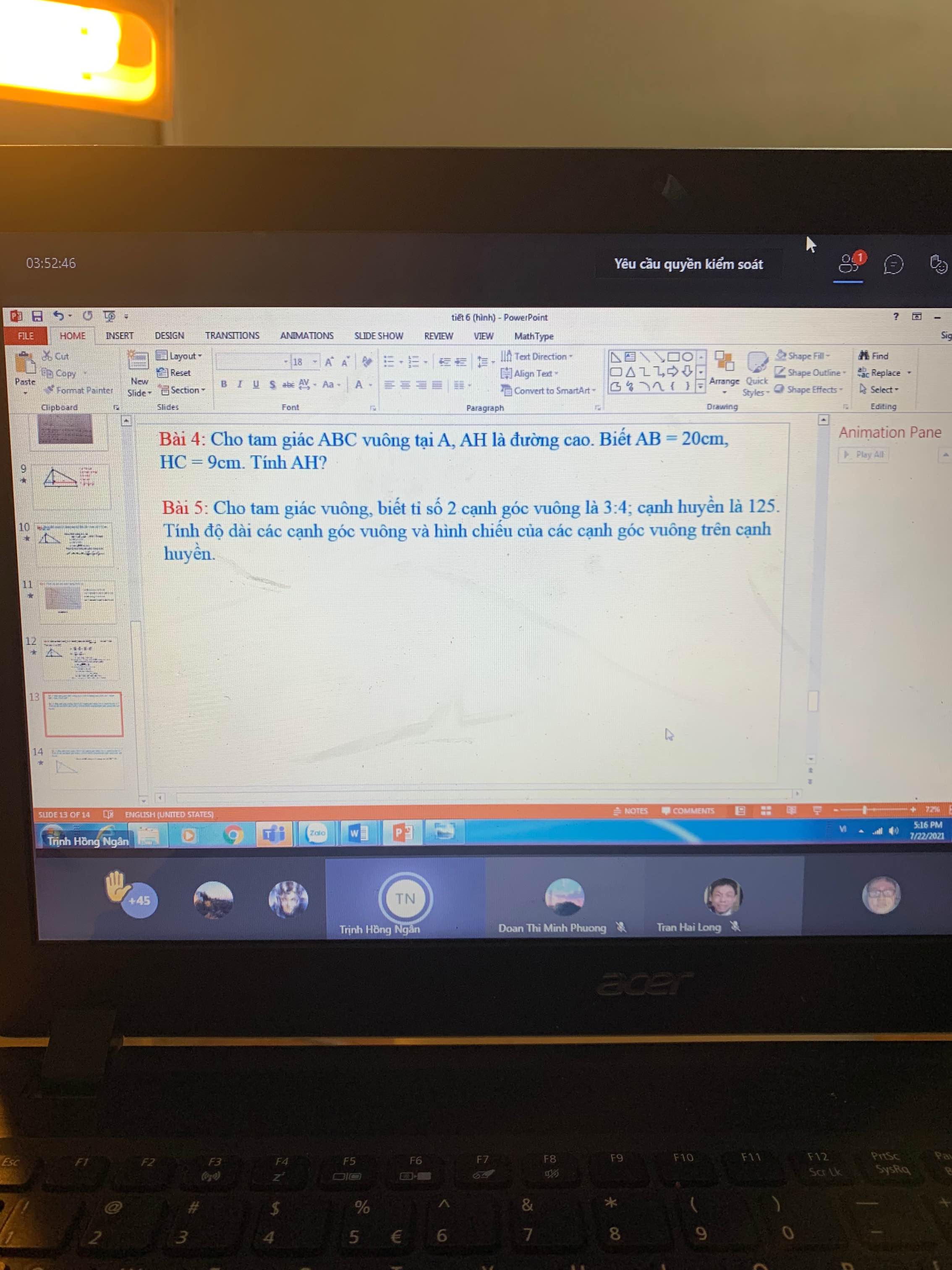
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\Leftrightarrow20^2=BH\left(BH+9\right)\)
\(\Leftrightarrow BH^2+9BH-400=0\Rightarrow\left[{}\begin{matrix}BH=16\\BH=-25\left(loại\right)\end{matrix}\right.\)
Áp dụng hệ thức lượng:
\(AH^2=BH.CH\Rightarrow AH=\sqrt{BH.CH}=12\)
5.
Gọi 3 cạnh tam giác vuông là a;b;c với \(\left\{{}\begin{matrix}a=125\\\dfrac{b}{c}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow b=\dfrac{3}{4}c\)
ĐỊnh lý Pitago:
\(a^2=b^2+c^2\Leftrightarrow125^2=\left(\dfrac{3}{4}c\right)^2+c^2\)
\(\Rightarrow c^2=10000\Rightarrow c=100\)
\(\Rightarrow b=\dfrac{3}{4}c=75\)
Hệ thức lượng:
\(b^2=a.b'\Rightarrow b'=\dfrac{b^2}{a}=45\)
\(c'=a-b'=80\)