Lấy giấy trắng cắt bốn tam giác vuông bằng nhau. Gọi a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của các tam giác vuông này. Cắt một hình vuông bằng tấm bìa có cạnh dài a+b. Dán bốn tam giác vuông lên tấm bìa như Hình 9.32
- Dùng ê ke kiểm tra phần bìa không bị che lấp có phải là hình vuông cạnh bằng c không. Từ đó tính diện tích phần bìa này theo c
- Tổng diện tích bốn tam giác vuông có độ dài hai cạnh góc vuông a, b là bao nhiêu?
- Diện tịch cả tấm bìa hình vuông cạnh a+ b bằng bao nhiêu?
- So sánh \({c^2} + 2{\rm{a}}b\) với \({\left( {a + b} \right)^2}\)để rút ra nhận xét về mối quan hệ giữa hai đại lượng \({c^2}\) và \({a^2} + {b^2}\).
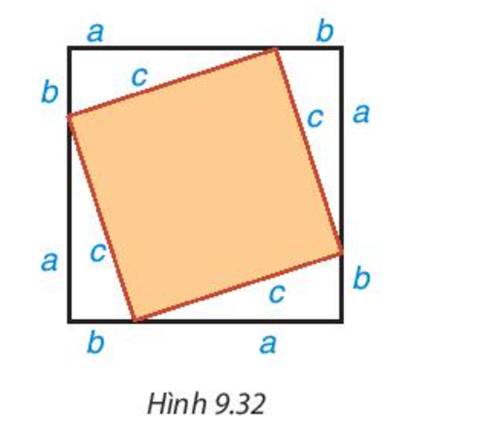
Phần bìa bị che lấp là hình vuông cạnh c. Diện tích của hình vuông là: \({c^2}\)
- Diện tích tấm bìa hình vuông là: \({\left( {a + b} \right)^2}\)
=> Diện tích bốn tam giác vuông là: \({\left( {a + b} \right)^2} - {c^2}\)
Tổng diện tích 4 tam giác vuông :
\(4.\dfrac{1}{2}a.b=2ab\)
Diện tích tấm bìa hình vuông :
\(\left(a+b\right).\left(a+b\right)=\left(a+b\right)^2\)
Ta thấy diện tích hình vuông cạnh c là \(c^2\)
mà \(\left(a+b\right)^2=c^2+2ab\)
\(\left(a+b\right)^2=a^2+b^2+2ab\)
\(\Rightarrow c^2=a^2+b^2\)