a) \(\left( {6{x^3} - 7{x^2} - x + 2} \right):\left( {2x + 1} \right)\)

b) $(x^4-x^3+x^2+3x):(x^2-2x+3)$

c) \(\left( {{x^2} + {y^2} + 6x + 9} \right):\left( {x + y + 3} \right)\)
\(=\left( {{x^2} + 6x + 9 - {y^2}} \right)\left( {x + y + 3} \right)\)
\(=\left[ {\left( {{x^2} + 2x.3 + {3^2}} \right) - {y^2}} \right]:\left( {x + y + 3} \right)\)
\(=\left[ {{{\left( {x + 3} \right)}^2} - {y^2}} \right]:\left( {x + y + 3} \right)\)
\(=\left( {x + 3 - y} \right)\left( {x + 3 + y} \right):\left( {x + y + 3} \right)\)
$= x + 3 - y$
$= x - y + 3$
(6x3 - 7x2 - x + 2) : (2x + 1)
= (6x3 + 3x2 - 10x2 - 5x + 4x + 2) : (2x + 1)
= [(6x3 + 3x2) - (10x2 + 5x) + (4x + 2)] : (2x + 1)
= [3x2(2x + 1) - 5x(2x + 1) + 2(2x + 1)] : (2x + 1)
= (3x2 - 5x + 2)(2x + 1) : (2x + 1)
= 3x2 - 5x + 2
(x4 - x3 + x2 + 3x) : (x2 - 2x + 3)
= (x4 + x3 - 2x3 - 2x2 + 3x2 + 3x) : (x2 - 2x + 3)
= [(x4 + x3) - (2x3 + 2x2) + (3x2 + 3x)] : (x2 - 2x + 3)
= [x3(x + 1) - 2x2(x + 1) + 3x(x + 1)] : (x2 - 2x + 3)
= (x3 - 2x2 + 3x)(x + 1) : (x2 - 2x + 3)
= x(x2 - 2x + 3)(x + 1): (x2 - 2x + 3)
= x(x + 1)
= x2 + x
(x2 - y2 + 6x + 9) : (x + y + 3)
= [(x2 + 6x + 9) - y2] : (x + y + 3)
= [(x + 3)2 - y2] : (x + y + 3)
= (x + 3 + y)(x + 3 - y) : (x + y + 3)
= (x + y + 3)(x - y + 3) : (x + y + 3)
= x - y + 3
CHÚC BN HOK TỐT ![]()
![]()
![]()
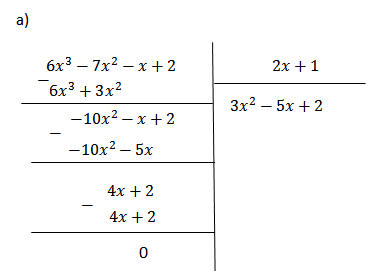
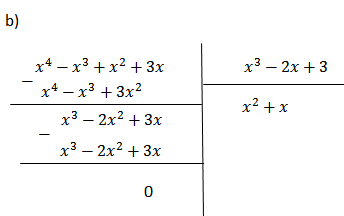
c) (x2+y2+6x+9):(x+y+3)
= (x2+6x+9−y2)(x+y+3)
= [(x2+2x.3+32)−y2]:(x+y+3)
= [(x+3)2−y2]:(x+y+3)
= (x+3−y)(x+3+y):(x+y+3)
= x + 3 - y
= x - y + 3
a) \(\dfrac{6x^3-7x^2-x+2}{2x+1}=\dfrac{6x^3-10x^2+4x+3x^2-5x+2}{2x+1}\)
\(=\dfrac{2x\left(3x^2-5x+2\right)+\left(3x^2-5x+2\right)}{2x+1}=\dfrac{\left(2x+1\right)\left(3x^2-5x+2\right)}{2x+1}\)
\(=3x^2-5x+2\)
b) \(\dfrac{x^4-x^3+x^2+3x}{x^2-2x+3}=\dfrac{x\left(x^3-x^2+x+3\right)}{x^2-2x+3}\)
\(=\dfrac{x\left(x^3-2x^2+3x+x^2-2x+3\right)}{x^2-2x+3}\)
\(=\dfrac{x\left(x\left(x^2-2x+3\right)+\left(x^2-2x+3\right)\right)}{x^2-2x+3}\)
\(=\dfrac{x\left(x+1\right)\left(x^2-2x+3\right)}{x^2-2x+3}=x\left(x+1\right)=x^2+x\)
c) \(\dfrac{x^2-y^2+6x+9}{x+y+3}=\dfrac{\left(x^2+6x+9\right)-y^2}{x+y+3}\)
\(=\dfrac{\left(x+3\right)^2-y^2}{x+y+3}=\dfrac{\left(x+3+y\right)\left(x+3-y\right)}{x+y+3}\)
\(=\dfrac{\left(x+y+3\right)\left(x-y+3\right)}{x+y+3}=x-y+3\)











