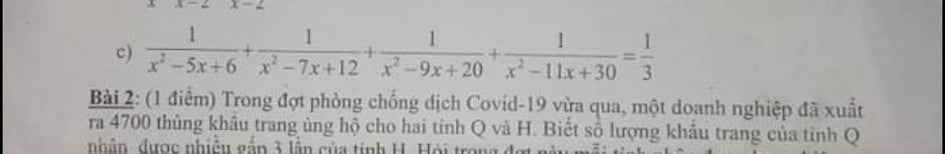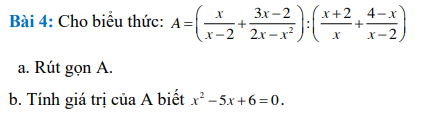Question

làm nhanh giúp  em câu

Answer 1

đk : x khác 2;3;4;5;6 

\(\dfrac{1}{\left(x-2\right)\left(x-3\right)}+\dfrac{1}{\left(x-3\right)\left(x-4\right)}+\dfrac{1}{\left(x-4\right)\left(x-5\right)}+\dfrac{1}{\left(x-5\right)\left(x-6\right)}=\dfrac{1}{3}\)

\(\Leftrightarrow\dfrac{1}{x-2}-\dfrac{1}{x-3}+\dfrac{1}{x-3}-\dfrac{1}{x-4}+...+\dfrac{1}{x-5}-\dfrac{1}{x-6}=\dfrac{1}{3}\)

\(\Leftrightarrow\dfrac{x-6-x+2}{\left(x-2\right)\left(x+6\right)}=\dfrac{1}{3}\Leftrightarrow-12=x^2+4x-12\)

\(\Leftrightarrow x\left(x+4\right)=0\Leftrightarrow x=0\left(tm\right);x=-4\left(tm\right)\)

Answer 2

Đk x khác 2,3,4,5,6

Phân tích các mẫu số ra ta được 

\(\dfrac{1}{\left(x-2\right)\left(x-3\right)}\) +\(\dfrac{1}{\left(x-3\right)\left(x-4\right)}\) \(\dfrac{1}{\left(x-4\right)\left(x-5\right)}\) +\(\dfrac{1}{\left(x-5\right)\left(x-6\right)}\) =\(\dfrac{1}{3}\)

<=>-(\(\dfrac{1}{x-2}\) -\(\dfrac{1}{x-3}\) +\(\dfrac{1}{x-3}\) -\(\dfrac{1}{x-4}\) +\(\dfrac{1}{x+4}\) -\(\dfrac{1}{x-5}\) +\(\dfrac{1}{x-5}\) -\(\dfrac{1}{x-6}\) )=\(\dfrac{1}{3}\)

<=>\(\dfrac{1}{x-2}\) -\(\dfrac{1}{x-6}\) =\(\dfrac{-1}{3}\)  

quy đồng khử mẫu được

<=>3(x-6)-3(x-2)+(x-2)(x-6)=0

<=>3x-18-3x+6+x^2-8x+12=0

<=>x(x-8)=0

<=>x=0;x=8

Vậy pt có tập nghiệm S=(0;8)