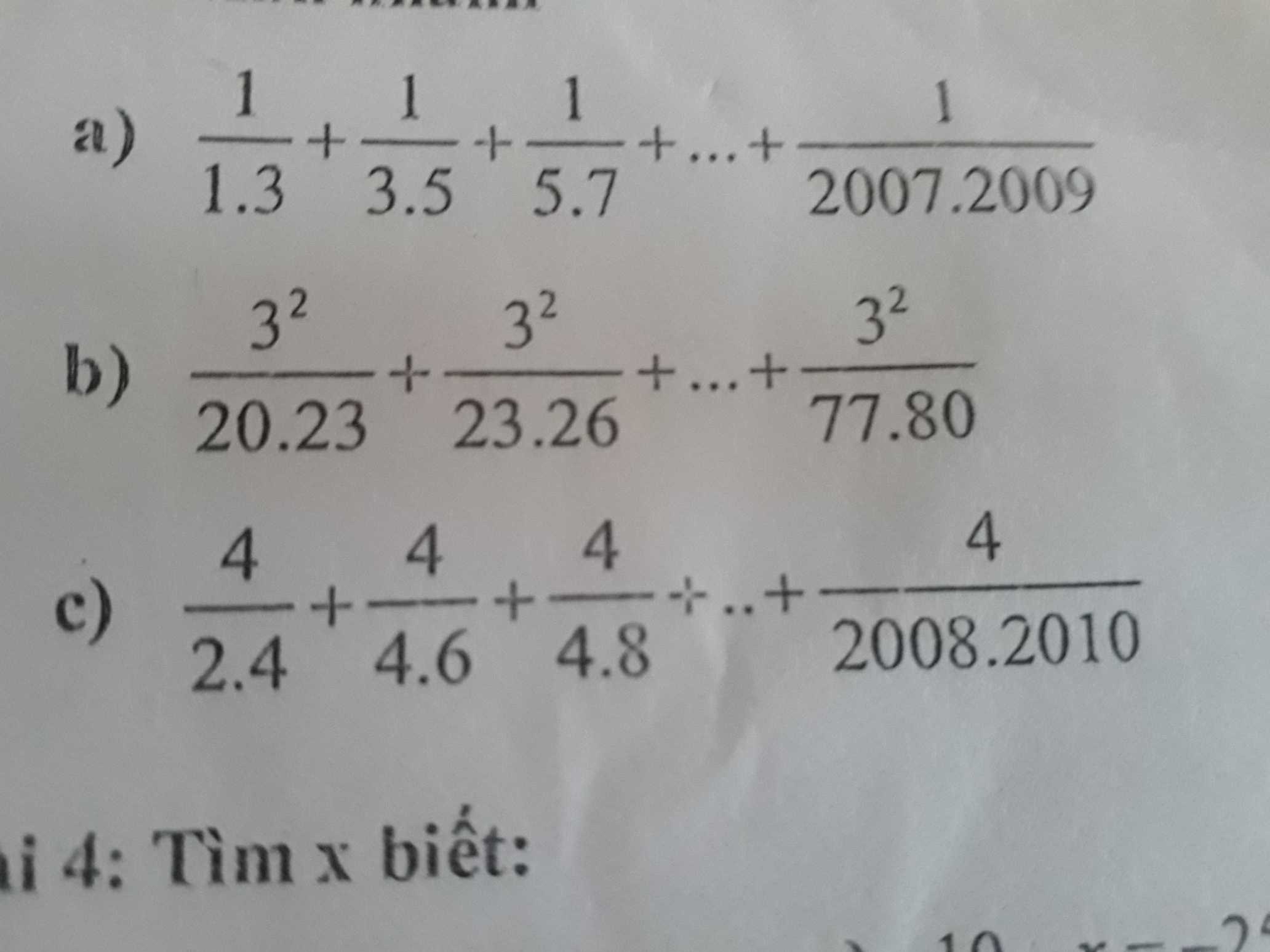Question

Hoe Hello me

Answer 1

a) Ta có: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{2007\cdot2009}\)

\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{2007\cdot2009}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2007}-\dfrac{1}{2009}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{2009}\right)\)

\(=\dfrac{1}{2}\cdot\dfrac{2008}{2009}=\dfrac{1004}{2009}\)

Answer 2

 

 

Answer 3

a)

\(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2007.2009}\)

\(=\dfrac{1}{2}\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{2007.2009}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2007}-\dfrac{1}{2009}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{2009}\right)=\dfrac{1}{2}.\dfrac{2008}{2009}=\dfrac{1004}{2009}\)

Answer 4

b)\(\dfrac{3^2}{20.23}+\dfrac{3^2}{23.26}+...+\dfrac{3^2}{77.80}\)

\(=\dfrac{3}{20}-\dfrac{3}{23}+\dfrac{3}{23}-\dfrac{3}{26}+...+\dfrac{3}{77}-\dfrac{3}{80}\)

\(=\dfrac{3}{20}-\dfrac{3}{80}=\dfrac{9}{80}\)