1: Xet ΔAHB có MK//BH
nên AM/AB=AK/AH
=>AK=1/3AH
2: Xét ΔABC có MN//BC
nên AM/AB=AN/AC
=>AM*AC=AB*AN
Đúng 1
Bình luận (0)
Bài 2: Định lý đảo và hệ quả của định lý Talet
Các câu hỏi tương tự
Cho ΔABC, đg cao AH. Lấy I tùy ý trên AH (≠ A, H). Đường thẳng BI cắt AC tại M; đường thẳng CI cắt AB tại N. Qua I kẻ d song2 vs BC, ns cắt AB, NH, MH, AC lần lượt tại E, R, S, F.
a) S2: \(\dfrac{IR}{IE}\) với \(\dfrac{CH}{CB}\); \(\dfrac{IS}{IF}\) với \(\dfrac{BH}{BC}\)
b) C/m rằng: RHS là Δ cân.
Bài 1:Cho tam giác ABC vuông tại A, đường cao AH và AB = 15cm, AC = 20cm. Gọi D là trung điểm của AB. Qua D kẻ DE vuông góc với BC tại E.
a) Tính BC, AH
Bài 1: Cho hình thang ABCD ( AB//CD) . O là giao của 2 đường chéo , qua O kể đường thẳng // với 2 đáy cắt AD tại M, cắt BC tại N. CMR : O là trung điểm của MN
Bài 2: Cho bigtriangleup{ABC} có S120 cm2 . Đường cao AH , trung tuyến AM , gọi G là trọng tâm của bigtriangleup{ABC}. Đường thẳng đi qua G//BC cắt AB, AH, AC lần lượt tại E, I, F
a) Tính dfrac{EF}{BC}và dfrac{AI}{AH}
b) SAEF?
Bài 3: Cho diamond{ABCD} , đường thẳng đi qua A// với BC cắt BD tại E ; đường thẳng đi qua B // với AD cắt AC...
Đọc tiếp
Bài 1: Cho hình thang ABCD ( AB//CD) . O là giao của 2 đường chéo , qua O kể đường thẳng // với 2 đáy cắt AD tại M, cắt BC tại N. CMR : O là trung điểm của MN
Bài 2: Cho \(\bigtriangleup{ABC}\) có S=120 cm2 . Đường cao AH , trung tuyến AM , gọi G là trọng tâm của \(\bigtriangleup{ABC}\). Đường thẳng đi qua G//BC cắt AB, AH, AC lần lượt tại E, I, F
a) Tính \(\dfrac{EF}{BC}\)và \(\dfrac{AI}{AH}\)
b) SAEF=?
Bài 3: Cho \(\diamond{ABCD}\) , đường thẳng đi qua A// với BC cắt BD tại E ; đường thẳng đi qua B // với AD cắt AC tại G
a) CM: EG//CD
b) Giả sử AB//CD . CM: AB2=CD.EG
cho ▲ ABC vuông tại A,có AB<AC,vẽ AH┸BC(H thuộc BC),trên cạnh HC lấy điểm M sao cho HM=HA.Qua M vẽ đường thẳng vuông góc với cạnh BC cắt AC tại I.Qua C vẽ đường thẳng vuông góc với cạnh BC cắt tia phân giác của góc IMC tại K.Chứng minh H,I,K thẳng hàng
Cho tam giác ABC cân tại A, BC = 8cm, phân giác của góc B cắt đường cáo AH ở K, AK/AH = 3/5 a) Tính độ dài AB b) Đường thẳn vuông góc với BK cắt AH ở E. Tính EH
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B, C và H (h.16)
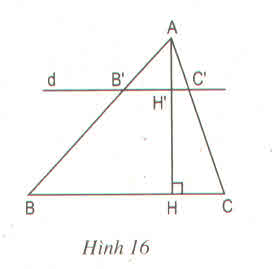
a) Chứng minh rằng :
dfrac{AH}{AH}dfrac{BC}{BC}
b) Áp dụng : Cho biết AHdfrac{1}{3}AH và diện tích tam giác ABC là 67,5cm^2. Tính diện tích tam giác ABC ?
Đọc tiếp
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H' (h.16)
a) Chứng minh rằng :
\(\dfrac{AH'}{AH}=\dfrac{B'C'}{BC}\)
b) Áp dụng : Cho biết \(AH'=\dfrac{1}{3}AH\) và diện tích tam giác ABC là \(67,5cm^2\). Tính diện tích tam giác AB'C' ?
Cho hình thang ABCD (AB//CD). Trên cạnh bên AD lấy điểm E sao cho dfrac{AE}{ED}dfrac{p}{q}. Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F (h.10)
Chứng minh rằng :
EFdfrac{p.CD+q.AB}{p+q}
Hướng dẫn : Kẻ thêm đường chéo AC, cắt EF ở , rồi áp dụng hệ quả của định lí Ta - let vào các tam giác ADC và CAB
Đọc tiếp
Cho hình thang ABCD (AB//CD). Trên cạnh bên AD lấy điểm E sao cho \(\dfrac{AE}{ED}=\dfrac{p}{q}\). Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F (h.10)
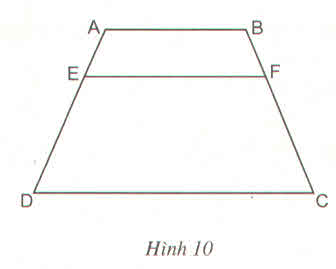
Chứng minh rằng :
\(EF=\dfrac{p.CD+q.AB}{p+q}\)
Hướng dẫn : Kẻ thêm đường chéo AC, cắt EF ở , rồi áp dụng hệ quả của định lí Ta - let vào các tam giác ADC và CAB
Cho tam giác ABC có AB = 9cm, AC = 12cm. Trên cạnh AB lấy điểm H và trên cạnh AC lấy điểm K sao cho AH = 6cm, AK=8cm
a/ Chứng minh: HK // BC
b/ Cho biết BC = 18cm. Tính HK
c, Gọi M là trung điểm BC , AM cắt HK tại I . Chứng minh I là trunng điểm của HK
nêu rõ cách giải
Cho H.thang ABCD. gọi E thuộc canh bên BC(E ở bất kì đâu trên BC). Qua C kẻ đường thẳng song song với AE cắt AD ở K. CMR BK//DE ( sử dụng đ.lí ta-lét đảo)