\(e,\Rightarrow\dfrac{9x+7}{9}\cdot\dfrac{3}{8}-\dfrac{x}{3}=\dfrac{11}{15}-\dfrac{61}{90}=\dfrac{1}{18}\\ \Rightarrow\dfrac{9x+7}{24}-\dfrac{x}{3}=\dfrac{1}{18}\\ \Rightarrow27x+21-24x=4\\ \Rightarrow3x=-17\Rightarrow x=-\dfrac{17}{3}\)
\(f,\Rightarrow\left[{}\begin{matrix}\dfrac{1}{7}x=\dfrac{2}{7}\\\dfrac{3}{5}x=\dfrac{1}{5}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
\(g,\Rightarrow\left|2x+3\right|< \dfrac{6}{21}:\dfrac{3}{7}=\dfrac{2}{3}\\ \Rightarrow-\dfrac{2}{3}< 2x+3< \dfrac{2}{3}\\ \Rightarrow-\dfrac{11}{3}< 2x< -\dfrac{7}{3}\\ \Rightarrow-\dfrac{11}{6}< x< -\dfrac{7}{6}\)
\(h,\Rightarrow\left|x-\dfrac{1}{5}\right|=-\dfrac{1}{2}:2=-\dfrac{1}{4}\\ \Rightarrow x\in\varnothing\left(\left|x-\dfrac{1}{5}\right|\ge0\right)\\ i,\Rightarrow\left|x+\dfrac{1}{2}\right|=\left|\dfrac{3}{4}x+1\right|\\ \Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}=\dfrac{3}{4}x+1\\x+\dfrac{1}{2}=-\dfrac{3}{4}x-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{6}{7}\end{matrix}\right.\)
\(k,\Rightarrow\left|3x+\dfrac{2}{5}\right|=x-\dfrac{3}{5}\\ \Rightarrow\left[{}\begin{matrix}3x+\dfrac{2}{5}=x-\dfrac{3}{5}\left(x\ge-\dfrac{2}{15}\right)\\3x+\dfrac{2}{5}=\dfrac{3}{5}-x\left(x< -\dfrac{2}{15}\right)\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\left(ktm\right)\\x=\dfrac{1}{20}\left(ktm\right)\end{matrix}\right.\\ \Rightarrow x\in\varnothing\)
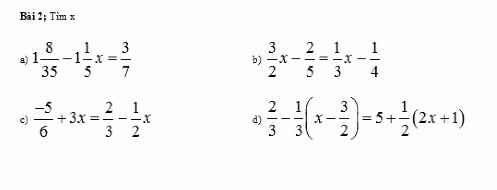
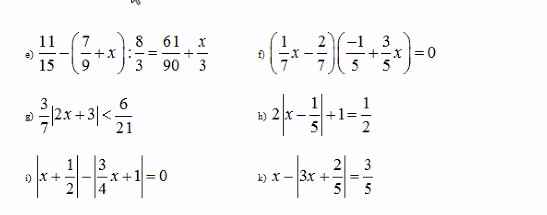
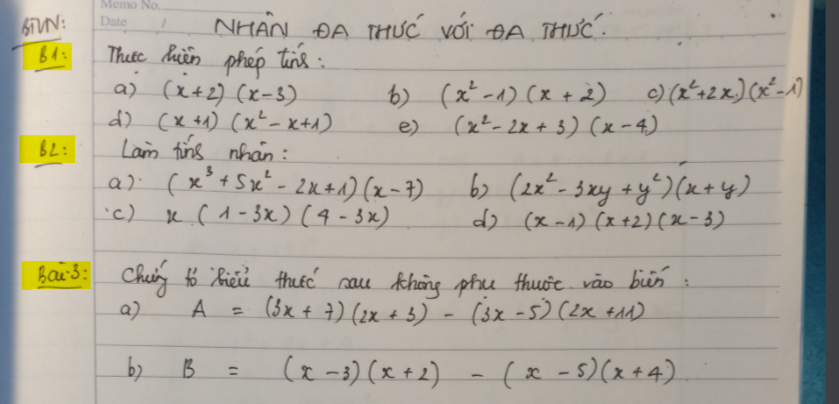
mn lm giúp mik vs ạ.Mik đang cần gấp ạ.Nhanh ạ