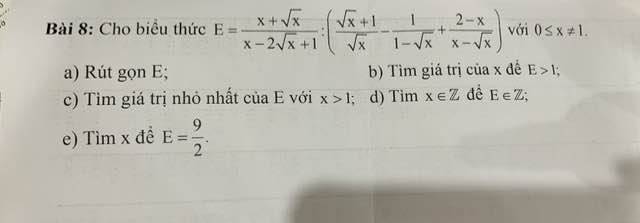a: \(E=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}:\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)+\sqrt{x}+2-x}{x-\sqrt{x}}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{x-1-x+\sqrt{x}+2}\)
\(=\dfrac{x\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}=\dfrac{x}{\sqrt{x}-1}\)
b; Để E>1 thì E-1>0
=>\(\dfrac{x-\sqrt{x}+1}{\sqrt{x}-1}>0\)
=>\(\sqrt{x}-1>0\)
=>x>1
c: \(E=\dfrac{x-1+1}{\sqrt{x}-1}=\sqrt{x}+1+\dfrac{1}{\sqrt{x}-1}\)
\(=\sqrt{x}-1+\dfrac{1}{\sqrt{x}-1}+2\)
=>\(E>=2\cdot\sqrt{\left(\sqrt{x}-1\right)\cdot\dfrac{1}{\sqrt{x}-1}}+2=4\)
Dấu = xảy ra khi \(\left(\sqrt{x}-1\right)^2=1\)
=>\(\left[{}\begin{matrix}\sqrt{x}-1=-1\\\sqrt{x}-1=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(nhận\right)\\x=0\left(loại\right)\end{matrix}\right.\)
d: Để E là số nguyên thì \(x⋮\sqrt{x}-1\)
=>\(x-1+1⋮\sqrt{x}-1\)
=>\(\sqrt{x}-1\in\left\{1;-1\right\}\)
=>\(\sqrt{x}\in\left\{2;0\right\}\)
=>\(x\in\left\{4;0\right\}\)
Kết hợp ĐKXĐ, ta được: x=4
e: E=9/2
=>\(\dfrac{x}{\sqrt{x}-1}=\dfrac{9}{2}\)
=>\(2x=9\sqrt{x}-9\)
=>\(2x-3\sqrt{x}-6\sqrt{x}+9=0\)
=>\(\left(2\sqrt{x}-3\right)\left(\sqrt{x}-3\right)=0\)
=>x=9 hoặc x=9/4
a) \(E=\dfrac{x+\sqrt{x}}{x-2\sqrt{x}+1}:\left(\dfrac{\sqrt{x}+1}{\sqrt{x}}-\dfrac{1}{1-\sqrt{x}}+\dfrac{2-x}{x-\sqrt{x}}\right)\)
\(E=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}:\left[\dfrac{\sqrt{x}+1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}+\dfrac{2-x}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]\)
\(E=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}:\left[\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{2-x}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]\)
\(E=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}:\dfrac{x-1+\sqrt{x}+2-x}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(E=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}:\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(E=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}+1}\)
\(E=\dfrac{x}{\sqrt{x}-1}\)
b) \(E>1\) khi:
\(\dfrac{x}{\sqrt{x}-1}>1\)
\(\Leftrightarrow\dfrac{x}{\sqrt{x}-1}-1>0\)
\(\Leftrightarrow\dfrac{x}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}-1}>0\)
\(\Leftrightarrow\dfrac{x-\sqrt{x}+1}{\sqrt{x}-1}>0\)
Mà:
\(x-\sqrt{x}+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
\(\Leftrightarrow\sqrt{x}-1>0\)
\(\Leftrightarrow\sqrt{x}>1\)
\(\Rightarrow x>1\)
c) Ta có:
\(E=\dfrac{x}{\sqrt{x}-1}\) với \(x>1\)
\(E=\dfrac{x-1+1}{\sqrt{x}-1}\)
\(E=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\)
\(E=\sqrt{x}+1+\dfrac{1}{\sqrt{x}-1}\)
\(E=\sqrt{x}-1+\dfrac{1}{\sqrt{x}-1}+2\)
\(\Rightarrow E\ge2\cdot\sqrt{\left(\sqrt{x}-1\right)\cdot\dfrac{1}{\sqrt{x}-1}}+2=2\cdot1+2=4\)
Dấu "=" xảy ra:
\(\left(\sqrt{x}-1\right)^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-1=1\\\sqrt{x}-1=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\left(ĐK:x>1\right)\)
Vậy: ...
d) \(E\in Z\) khi:
\(\dfrac{x}{\sqrt{x}-1}=\dfrac{x-1+1}{\sqrt{x}-1}=\sqrt{x}+1+\dfrac{1}{\sqrt{x}-1}\in Z\)
\(\Rightarrow1\) ⋮ \(\sqrt{x}-1\)
\(\Rightarrow\sqrt{x}-1\) \(\in\) Ư(1)
Mà: \(Ư\left(1\right)=\left\{1;-1\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{2;0\right\}\)
\(\Rightarrow x\in\left\{4;0\right\}\)
Vậy: ...
e) \(E=\dfrac{9}{2}\) khi:
\(\dfrac{x}{\sqrt{x}-1}=\dfrac{9}{2}\)
\(\Leftrightarrow2x=9\sqrt{x}-9\)
\(\Leftrightarrow2x-9\sqrt{x}+9=0\)
\(\Leftrightarrow2x-6\sqrt{x}-3\sqrt{x}+9\)
\(\Leftrightarrow2\sqrt{x}\left(\sqrt{x}-3\right)-3\left(\sqrt{x}-3\right)=0\)
\(\Leftrightarrow\left(2\sqrt{x}-3\right)\left(\sqrt{x}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-3=0\\2\sqrt{x}-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\\2\sqrt{x}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3^2\\x=\left(\dfrac{3}{2}\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\left(tm\right)\\x=\dfrac{9}{4}\left(tm\right)\end{matrix}\right.\)