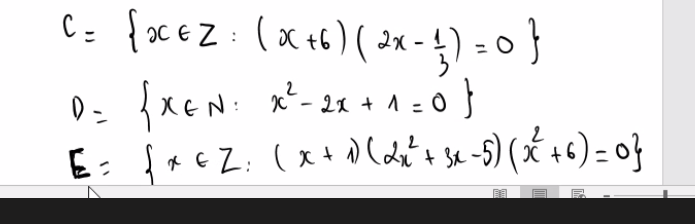Bài 1:
ĐKXĐ:
a/\(\left\{{}\begin{matrix}x-2\ne0\\4-x\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne2\\x\le4\end{matrix}\right.\) hay \(D=[4;+\infty)\backslash\left\{2\right\}\)
b \(\left\{{}\begin{matrix}x-1\ge0\\x\ne0\\3-x>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne0\\x< 3\end{matrix}\right.\) \(\Rightarrow1\le x< 3\) hay \(D=[1;3)\)
c/ \(\left\{{}\begin{matrix}x\ge0\\x^2-x-20\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge0\\x\ne5\\x\ne-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge0\\x\ne5\end{matrix}\right.\Rightarrow D=[0;+\infty)\backslash\left\{5\right\}\)
d/ \(2-x\left|x\right|>0\Rightarrow x\left|x\right|< 2\Rightarrow\left[{}\begin{matrix}x< 0\\x< \sqrt{2}\end{matrix}\right.\) \(\Rightarrow x< \sqrt{2}\)
\(D=\left(-\infty;\sqrt{2}\right)\)
e/ Do \(x^2-x+1=x^2-x+\frac{1}{4}+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}>0\)
Nên hàm số xác định khi \(x+\sqrt{x^2-x+1}\ge0\Leftrightarrow\sqrt{x^2-x+1}\ge-x\) (1)
- Với \(x\ge0\Rightarrow\left\{{}\begin{matrix}-x\le0\\\sqrt{x^2-x+1}>0\end{matrix}\right.\) nên (1) hiển nhiên đúng
- Với \(x< 0\) hai vế của (1) đều dương, bình phương ta được:
\(x^2-x+1>x^2\Rightarrow x< 1\) (đúng \(\forall x< 0\))
Vậy hàm số xác định trên R hay D=R
f/ \(\left\{{}\begin{matrix}x+2\ge0\\\left|x+1\right|-1\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge-2\\\left|x+1\right|\ne1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge-2\\x+1\ne1\\x+1\ne-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\ne0\\x\ne-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>-2\\x\ne0\end{matrix}\right.\) \(\Rightarrow D=\left(-2;+\infty\right)\backslash\left\{0\right\}\)
g/ \(\left\{{}\begin{matrix}x\ge0\\x-2\sqrt{x}-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge0\\\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\) \(\Rightarrow D=[0;+\infty)\backslash\left\{9\right\}\)
h/ \(\left\{{}\begin{matrix}x-1\ge0\\x-2\ne0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne2\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{2;3\right\}\)
i/ \(\left\{{}\begin{matrix}x\ne0\\1+x>0\\1-x\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne0\\x>-1\\x\le1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-1< x\le1\\x\ne0\end{matrix}\right.\)
\(D=(-1;1]\backslash\left\{0\right\}\)
j/ \(1-2\left|x\right|\ge0\Rightarrow2\left|x\right|\le1\Rightarrow\left|x\right|\le\frac{1}{2}\Rightarrow-\frac{1}{2}\le x\le\frac{1}{2}\)
\(D=\left[-\frac{1}{2};\frac{1}{2}\right]\)
Bài 4:
a/ \(\left\{{}\begin{matrix}x+m\ge0\\2x-m+1\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge-m\\x\ge\frac{m-1}{2}\end{matrix}\right.\)
Để hàm số xác định với mọi \(x>0\)
\(\Rightarrow\left\{{}\begin{matrix}-m\le0\\\frac{m-1}{2}\le0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ge0\\m\le1\end{matrix}\right.\Rightarrow0\le m\le1\)
b/ \(\left\{{}\begin{matrix}2x-3m+4\ge0\\x+m-1\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge\frac{3m-4}{2}\\x\ne m-1\end{matrix}\right.\)
Để hàm số xác đinh với mọi \(x>0\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{3m-4}{2}\le0\\m-1\le0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m\le\frac{4}{3}\\m\le1\end{matrix}\right.\Rightarrow m\le1\)
Bài 5:
Trùng với bài 3
Bài 6:
a/ TXĐ: \(-2\le x\le2\)
b/
+/ Ta có \(-2< -1< 0\) nên \(f\left(-1\right)=1-\left(-1\right)=2\)
+/ \(0=0\Rightarrow f\left(0\right)=0\)
+/ \(0< \frac{3}{2}< 2\Rightarrow f\left(\frac{3}{2}\right)=\frac{3}{2}\)
Không nhìn rõ mẫu là 2 hay 8
sai rồi bn ơi x^2-x+1>x^2 lm sao => x<1 đc nhảm nhí
Bài 2:
ĐKXĐ: \(\left\{{}\begin{matrix}x+m-1\ge0\\2m-x>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge-m+1\\x< 2m\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-m+1\le x< 2m\\2m>-m+1\end{matrix}\right.\) \(D=[-m+1;2m)\) với \(m>\frac{1}{3}\)
Để hàm số xác định trên \(\left(-1;3\right)\Rightarrow\left(-1;3\right)\subset D\)
\(\Rightarrow\left\{{}\begin{matrix}-m+1\le-1\\2m\ge3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ge2\\m\ge\frac{3}{2}\end{matrix}\right.\) \(\Rightarrow m\ge2\)
Bài 3:
ĐKXĐ: \(\left\{{}\begin{matrix}x+m>0\\-x-2m+6\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>-m\\x\le-2m+6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-m< x\le-2m+6\\-2m+6>-m\end{matrix}\right.\) \(\Rightarrow D=(-m;-2m+6]\) với \(m< 6\)
Để hàm số xác định trên \(\left(-1;0\right)\Rightarrow\left(-1;0\right)\subset D\)
\(\Rightarrow\left\{{}\begin{matrix}-m\le-1\\-2m+6\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ge1\\m\le3\end{matrix}\right.\) \(\Rightarrow1\le m\le3\)