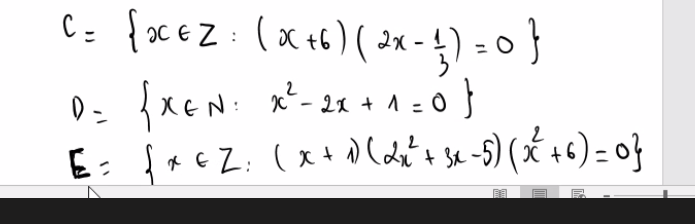10/
\(B\cup C=\left[-2;5\right]\) ; \(A\cap C=[-2;3)\)
\(\Rightarrow\left(B\cup C\right)\backslash\left(A\cap C\right)=\left[3;5\right]\)
11/
Để \(A\cap B=\varnothing\Rightarrow\left[{}\begin{matrix}2a\ge5\\3a+1< 0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}a\ge\frac{5}{2}\\a< -\frac{1}{3}\end{matrix}\right.\)
\(\Rightarrow\) Để \(A\cap B\ne\varnothing\Rightarrow-\frac{1}{3}\le a< \frac{5}{2}\)
12/
\(A\cup B=R\Rightarrow\left(A\cup B\right)\backslash C=(-\infty;0]\cup\left(1;+\infty\right)\)
\(A\cap B=\left\{1\right\}\Rightarrow A\cap B\cap C=\left\{1\right\}\) (sai)
\(A\cup B=R=\left(-\infty;+\infty\right)\Rightarrow A\cup B\cup C=\left(-\infty;+\infty\right)\)
\(\left(A\cap B\right)=\left\{1\right\}\Rightarrow\left(A\cap B\right)\backslash C=\varnothing\)
13/
Để \(A\cup B=R\Leftrightarrow m+1\ge-1\Rightarrow m\ge-2\)
14/
\(A\cap B=[-1;3)\Rightarrow R\backslash\left(A\cap B\right)=\left(-\infty;-1\right)\cup[3;+\infty)\)
15/
\(A\cap B=[0;3)\) ; \(A\backslash B=\left(-1;0\right)\)
\(\Rightarrow\left(A\cap B\right)\cup\left(A\backslash B\right)=\left(-1;3\right)\)
16/
\(A=\left(-\infty;-10\right)\cup\left(10;+\infty\right)\cup\left\{0\right\}\)
\(\Rightarrow R\backslash A=[-10;0)\cup(0;10]\) hay \(\left[-10;10\right]\backslash\left\{0\right\}\)
17/
\(A=\left(-\infty;-2\right)\) ; \(B=(-\infty;4)\) \(\Rightarrow A\subset B\)
\(B\backslash A=[-2;4)\)
18/
Số tập con có 2 phần tử của X là: \(C_{n+1}^2=\frac{n\left(n+1\right)}{2}\)
// Nếu chưa học toán học tổ hợp thì giải dài dòng văn tự như sau:
Gọi tập hợp X có dạng \(X=\left\{a_0;a_1;...;a_n\right\}\)
Với mỗi phần tử của X, ví dụ \(a_0\) luôn có \(n\) cách ghép cặp với một phần tử khác để tạo thành tập hợp gồm 2 phần tử (ví dụ \(\left(a_0;a_1\right);\left(a_0;a_2\right)....;\left(a_0;a_n\right)\)
Do tập X có \(n+1\) phần tử nên sẽ có \(n\left(n+1\right)\) tập hợp con được tạo ra như vậy
Nhưng mỗi một cặp số hay mỗi tập con sẽ bị xuất hiện 2 lần (ví dụ ghép \(\left(a_0;a_1\right)\) thì sau đó khi dùng \(a_1\) sẽ xuất hiện \(\left(a_1;a_0\right)\) giống tập hợp trên)
Do đó số tập con có 2 phần tử được tạo ra là: \(\frac{n\left(n+1\right)}{2}\)