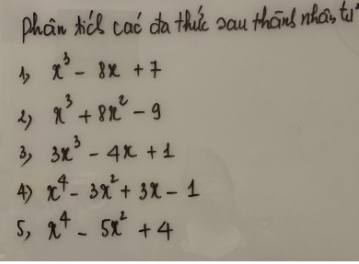3)Tìm GTNN
a)\(x^2+2x+3\)
\(=\left(x^2+2x+1\right)+2\)
\(=\left(x+1\right)^2+2\)
Vì \(\left(x+1\right)^2\ge0\)
Nên \(\left(x+1\right)^2+2\ge2\)
Vậy GTNN của \(x^2+2x+3\) là 2 tại \(x=1\)
2)Tìm x, biết
b)\(16x^2-\left(4x-5\right)^2=15\)
\(\Leftrightarrow\left(4x\right)^2-\left(4x-5\right)^2-15=0\)
\(\Leftrightarrow\left(4x-4x+5\right)\left(4x+4x-5\right)-15=0\)
\(\Leftrightarrow5\left(8x-5\right)-15=0\)
\(\Leftrightarrow40x-25-15=0\)
\(\Leftrightarrow40x-40=0\)
\(\Leftrightarrow40\left(x-1\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=40\\x-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=40\\x=1\end{matrix}\right.\)
3) tìm GTNN
b)\(x^2-4x+5\)
\(=x^2-4x+4+1\)
\(=x^2-2.x.2+2^2+1\)
\(=\left(x-2\right)^2+1\)
Vì \(\left(x-2\right)^2\ge0\)
Nên\(\left(x-2\right)^2+1\ge1\)
Vậy GTNN của \(x^2-4x+5\) là 1 tại \(x=2\)
3)Tìm GTNN
b)\(x^2-4x+5\)
\(=x^2-2.x.2+2+3\)
\(=\left(x-2\right)^2+3\)
Vì \(\left(x-2\right)^2\ge0\)
Nên \(\left(x-2\right)^2+3\ge3\)
Vậy GTNN cảu \(x^2-4x+5\) là 3 tại \(x=2\)
2)Tìm x, biết:
a) \(\left(2x+3\right)^2-4\left(x-1\right)\left(x+1\right)=49\)
\(\Leftrightarrow\left[\left(2x\right)^2+2.2x.3+3^2\right]-4\left(x^2-1^2\right)-49=0\)
\(\Leftrightarrow\left(4x^2+12x+9\right)-\left(4x^2-4\right)-49=0\)
\(\Leftrightarrow4x^2+12x+9-4x^2+4-49=0\)
\(\Leftrightarrow12x-36=0\)
\(\Leftrightarrow12x=36\)
\(\Leftrightarrow x=3\)
Vậy x=3