thôi trình bày lại.
\(VT=3+\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}+\dfrac{y^2}{z^2}+\dfrac{z^2}{y^2}+\dfrac{x^2}{z^2}+\dfrac{z^2}{x^2}\)
\(=3+\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)+\left(\dfrac{y^2}{z^2}+\dfrac{x^2}{z^2}\right)+\left(\dfrac{z^2}{y^2}+\dfrac{z^2}{x^2}\right)\)
Áp dụng BĐT AM-GM:
\(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\ge2\)
Áp dụng BĐT bunyakovsky:\(\dfrac{y^2}{z^2}+\dfrac{x^2}{z^2}\ge\dfrac{1}{2}\left(\dfrac{x+y}{z}\right)^2\)
\(\dfrac{z^2}{y^2}+\dfrac{z^2}{x^2}\ge\dfrac{1}{2}\left(\dfrac{z}{y}+\dfrac{z}{x}\right)^2\ge\dfrac{1}{2}.\left(\dfrac{4z}{x+y}\right)^2=8\left(\dfrac{z}{x+y}\right)^2\)
(\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\))
khi đó \(VT\ge5+\dfrac{1}{2}\left(\dfrac{x+y}{z}\right)^2+8\left(\dfrac{z}{x+y}\right)^2\)
đặt \(\dfrac{z}{x+y}=a\)thì \(a\ge1\left(z\ge x+y\right)\)
\(VT=5+8a^2+\dfrac{1}{2a^2}=\left(\dfrac{1}{2a^2}+\dfrac{a^2}{2}\right)+\dfrac{15a^2}{2}+5\ge\left(\dfrac{1}{2a^2}+\dfrac{a^2}{2}\right)+\dfrac{25}{2}\)
Áp dụng BĐT AM-GM:\(\dfrac{1}{2a^2}+\dfrac{a^2}{2}\ge2\sqrt{\dfrac{a^2}{4a^2}}=1\)
do đó \(VT\ge1+\dfrac{25}{2}=\dfrac{27}{2}\)
dấu = xảy ra khi \(a=1\Leftrightarrow x=y=\dfrac{z}{2}\)
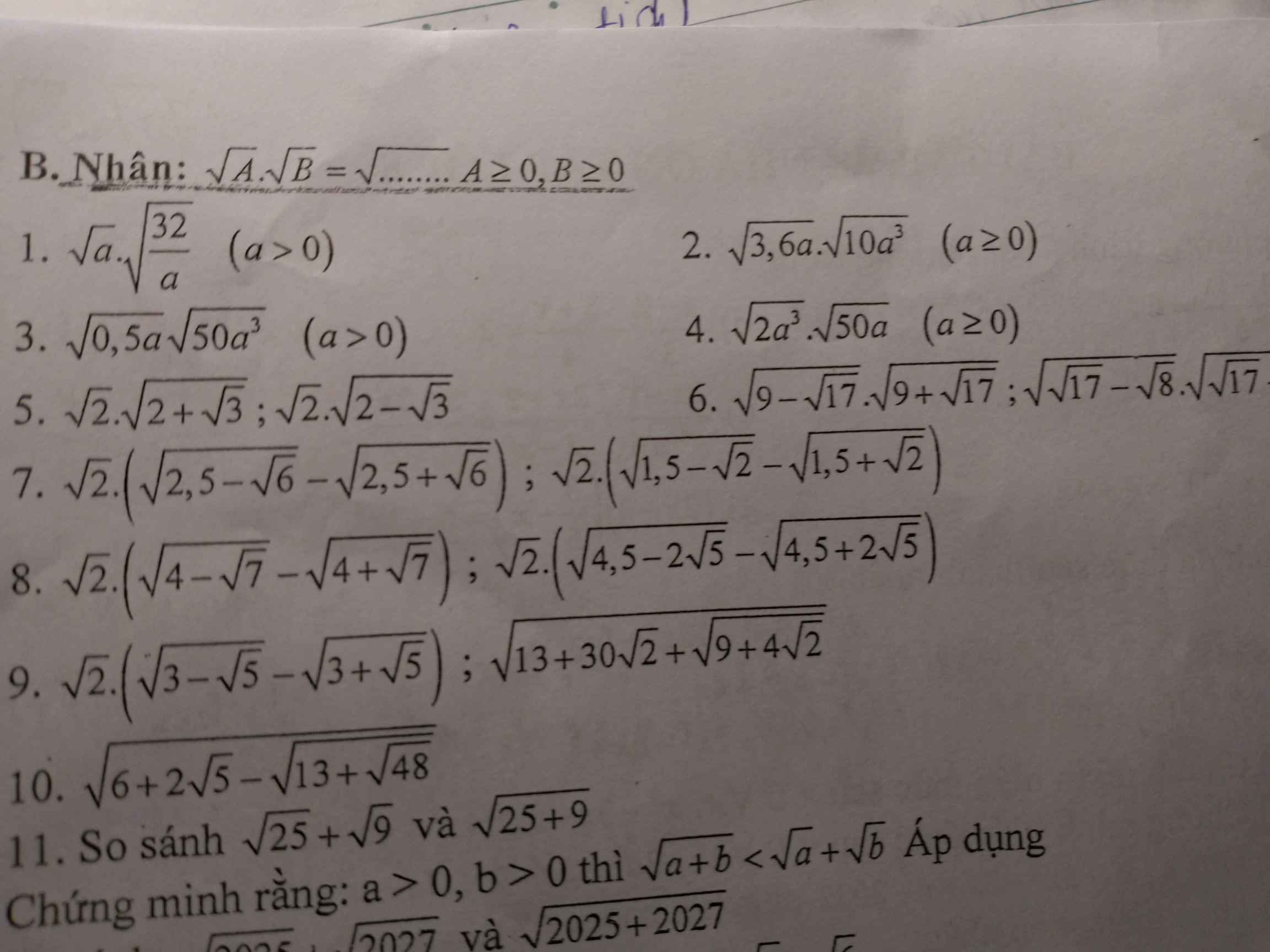
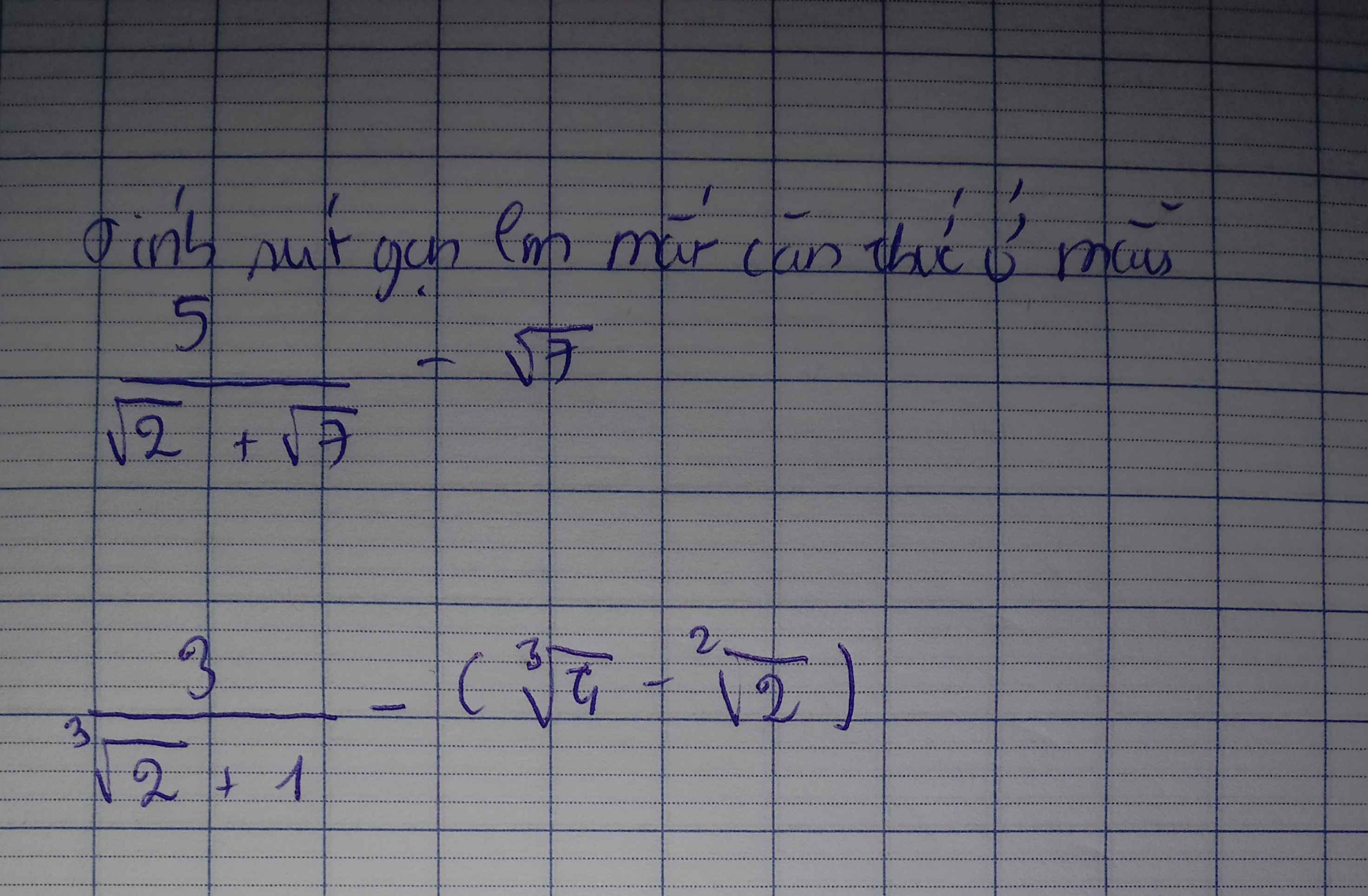
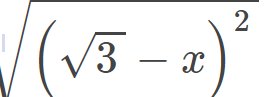
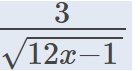GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
