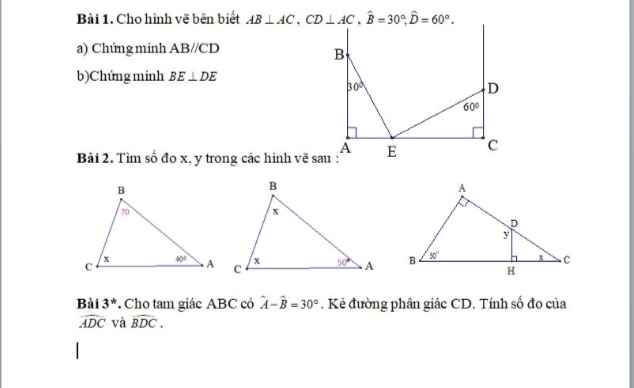
Bài 1:
a. $AB\perp AC, CD\perp AC$
$\Rightarrow AB\parallel CD$
b.Áp dụng định lý về tổng 3 góc trong tam giác ta có:
$\widehat{BEA}=90^0-\widehat{ABE}=90^0-30^0=60^0$
$\widehat{DEC}=90^0-\widehat{EDC}=90^0-60^0=30^0$
$\Rightarrow \widehat{BEA}+\widehat{DEC}=60^0+30^0=90^0$
$\widehat{BED}=180^0-(\widehat{BEA}+\widehat{DEC})$
$=180^0-90^0=90^0$
$\Rightarrow BE\perp ED$
(đpcm)
Bài 2:
Áp dụng định lý về tổng 3 góc trong tam giác ta có:
a.
$\widehat{A}+\widehat{B}+\widehat{C}=180^0$
$40^0+70^0+x=180^0$
$x=180^0-110^0=70^0$
b.
$\widehat{A}+\widehat{B}+\widehat{C}=180^0$
$50^0+x+x=180^0$
$2x=130^0$
$x=65^0$
c.
$\widehat{A}+\widehat{B}+\widehat{C}=180^0$
$90^0+30^0+x=180^0$
$x=180^0-120^0=60^0$
$y=180^0-\widehat{DHC}=\widehat{DHC}+\widehat{DCH}$
$=90^0+30^0=120^0$
Bài 3:
Ta thấy:
$\widehat{ADC}=\widehat{B}+\widehat{BCD}=\widehat{B}+\frac{1}{2}\widehat{C}$
$\widehat{BDC}=\widehat{A}+\widehat{ACD}=\widehat{A}+\frac{1}{2}\widehat{C}$
$\Rightarrow \widehat{BDC}-\widehat{ADC}=\widehat{A}-\widehat{B}=30^0$
Mà: $\widehat{BDC}+\widehat{ADC}=180^0$
Do đó:
$\widehat{BDC}=(180^0+30^0):2=105^0$
$\widehat{ADC}=(180^0-30^0):2=75^0$






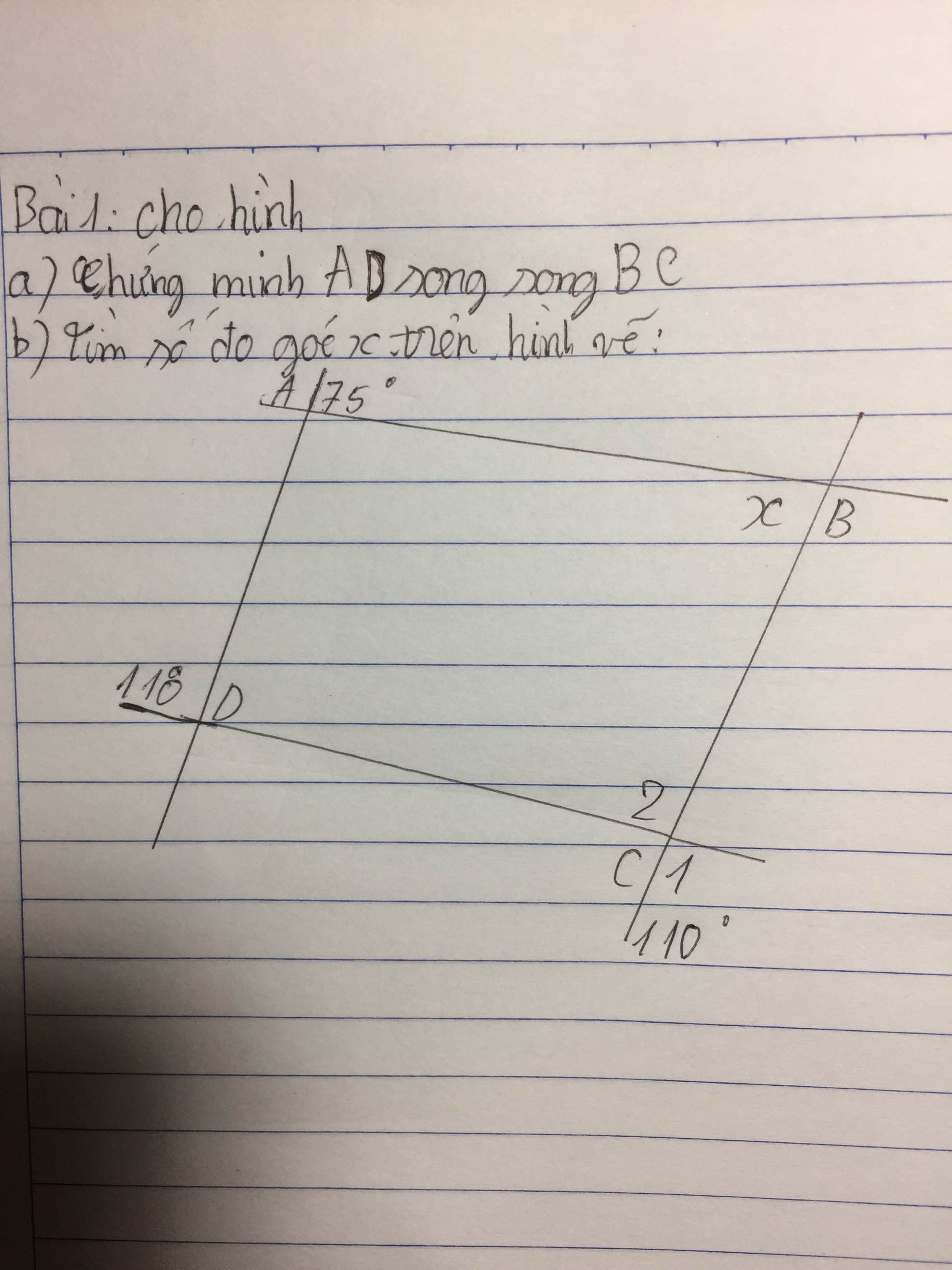




 mọi người giúp em với
mọi người giúp em với