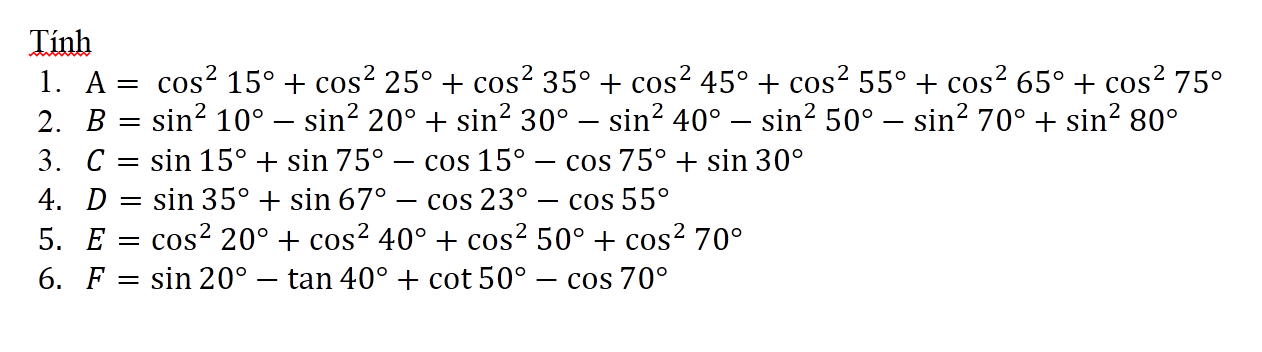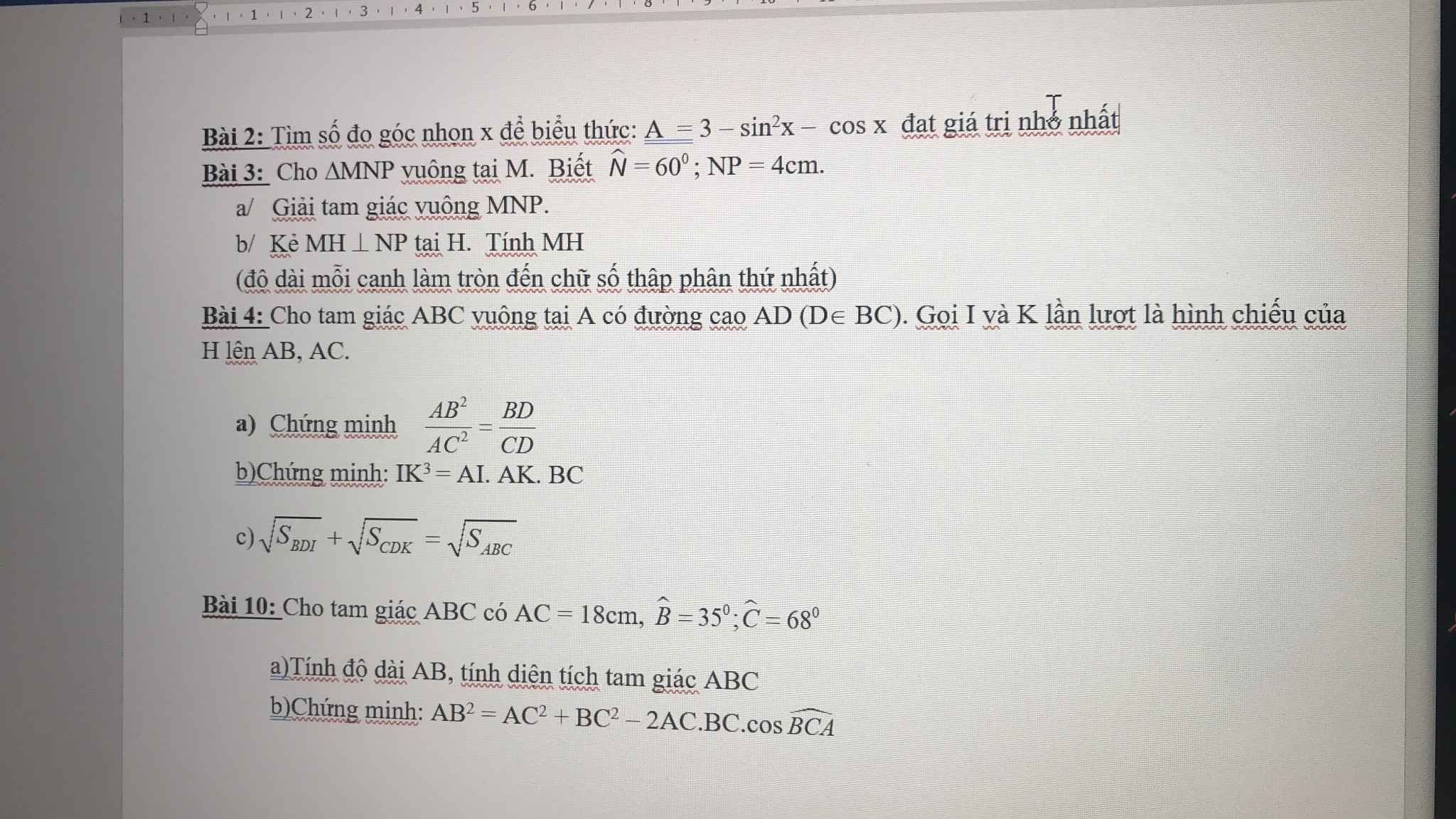Question

giúp mình với 

Answer 1

Bài 2 :

a, Áp dụng định lí Pytago tam giác ABC vuông tại A

\(BC^2=AB^2+AC^2=25+144=169\Rightarrow BC=13\)cm 

b, sinC = AB/BC = 5/13

cosC = AC/BC = 12/13

tanC = AB/AC = 5/12

cotaC = AC/AB = 12/5

c,  sinB = AC/BC = 12/13

cosB  = AB/BC = 5/13

tanB = AC/AB = 12/5 

cotaB = AB/AC = 5/12 

Answer 2

Bài 3: 

a) Xét ΔABC có \(BC^2=AB^2+AC^2\left(15^2=9^2+12^2\right)\)

nên ΔABC vuông tại A(Định lí Pytago đảo)

c) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:

\(AE\cdot AB=AH^2\)(1)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HI là đường cao ứng với cạnh huyền AC, ta được:

\(AI\cdot AC=AH^2\)(2)

Từ (1) và (2) suy ra \(AE\cdot AB=AI\cdot AC\)