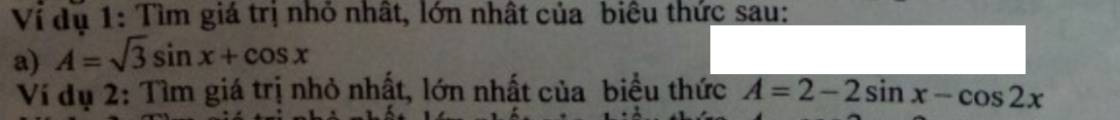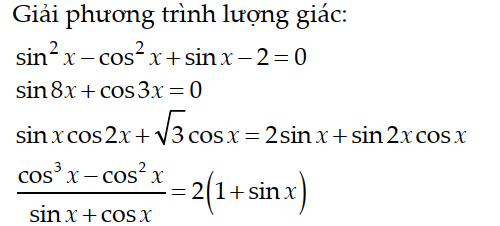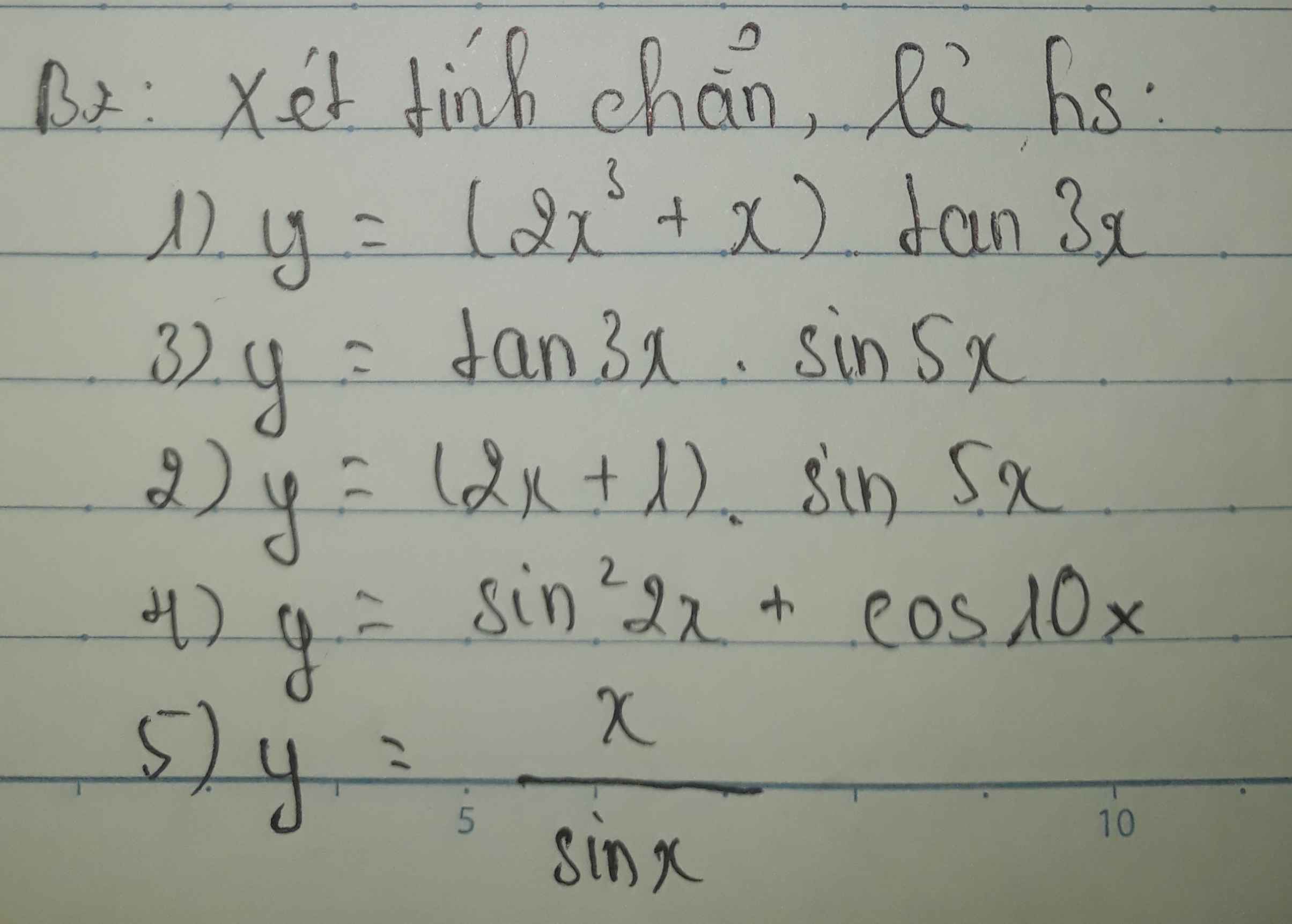Ví dụ 1:
a)
Đạo hàm của biểu thức A theo x:
`A' = (√3cosx - sinx)`
Giải phương trình A' = 0:
`(√3cosx - sinx) = 0`
`⇒ √3cosx = sinx`
`⇒ 3cos^2x = sin^2x` (bình phương hai vế)
`⇒ 3(1 - sin^2x) = sin^2x` (sử dụng công thức `cos^2x = 1 - sin^2x`)
`⇒ 3 - 3sin^2x = sin^2x`
`⇒ 4sin^2x = 3`
`⇒ sin^2x = 3/4`
`⇒ sinx = ±√(3/4) = ±√3/2`
Với `sinx = √3/2`, ta có `cosx = √(1 - sin^2x) = √(1 - 3/4) = √1/4 = 1/2`
Với `sinx = -√3/2`, ta có `cosx = √(1 - sin^2x) = √(1 - 3/4) = √1/4 = 1/2`
Vậy, giá trị nhỏ nhất của biểu thức A là:
`A(min) = √3sinx + cosx = √3(√3/2) + 1/2 = 3/2 + 1/2 = 2`
Giá trị lớn nhất của biểu thức A cũng là `2`