Kẻ Pz//Mx//Ny
\(\Rightarrow\left\{{}\begin{matrix}\widehat{MPz}+\widehat{PMx}=180^0\\\widehat{NPz}+\widehat{PNy}=180^0\end{matrix}\right.\)(trong cùng phía)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{MPz}=180^0-\widehat{PMx}=180^0-120^0=60^0\\\widehat{NPz}=180^0-\widehat{PNy}=180^0-130^0=50^0\end{matrix}\right.\)
\(\Rightarrow\widehat{MPN}=\widehat{MPz}+\widehat{NPz}=60^0+50^0=110^0\)
Kẻ Pz//Mx//Ny
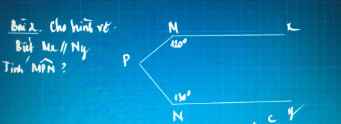
\(\Rightarrow\left\{{}\begin{matrix}\widehat{xMP}+\widehat{MPz}=180^0\\\widehat{yNP}+\widehat{NPz}=180^0\end{matrix}\right.\left(trong.cùng.phía\right)\\ \Rightarrow\left\{{}\begin{matrix}\widehat{MPz}=180^0-120^0=60^0\\\widehat{NPz}=180^0-150^0=30^0\end{matrix}\right.\\ \Rightarrow\widehat{MPN}=\widehat{MPz}+\widehat{NPz}=90^0\)
Qua P kẻ PQ sao cho PQ//Mx (1)
Vì PQ//Mx => PMx + P1 = 1800 (trong cùng phía)
=> P1 = 1800 - 1200 = 600
Theo đề lại có Mx//Ny (2)
(1), (2) => PQ//Ny
=> PNy + P2 = 1800 (trong cùng phía)
=> P2 = 1800 - 1300 = 500
Ta có P = P1 + P2 = 500 + 600 = 1100