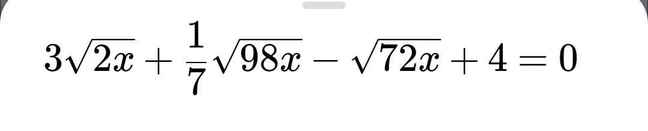ĐKXĐ: \(x\ge5\)
\(\sqrt{x^2-25}-\sqrt{x-5}=0\)
<=>\(\sqrt{\left(x+5\right)\left(x-5\right)}-\sqrt{x-5}=0\)
<=>\(\sqrt{x+5}.\sqrt{x-5}-\sqrt{x-5}=0\)
<=>\(\sqrt{x-5}\left(\sqrt{x+5}-1\right)=0\)
<=>\(\left[{}\begin{matrix}\sqrt{x-5}=0\\\sqrt{x+5}-1=0\end{matrix}\right.\)
<=>\(\left[{}\begin{matrix}x=5\\x=-4\end{matrix}\right.\)
Kết hợp với ĐKXĐ ta có x = 5 là nghiệm duy nhất của phương trình.
đk để x được xát định là \(x\ge5\)
\(\sqrt{x^2-25}-\sqrt{x-5}=0\) \(\Leftrightarrow\) \(\sqrt{x^2-25}=\sqrt{x-5}\)
\(\Leftrightarrow\) \(x^2-25=x-5\) \(\Leftrightarrow\) \(x^2-x-20=0\)
\(\Delta\) = \(1^2-4.\left(-20\right)=1+80=81>0\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{1+\sqrt{81}}{2}=\dfrac{1+9}{2}=\dfrac{10}{2}=5\left(tmđk\right)\)
\(x_2=\dfrac{1-\sqrt{81}}{2}=\dfrac{1-9}{2}=\dfrac{-8}{2}=-4\left(loại\right)\)
vậy \(x=5\)
\(\sqrt{x^2-25}-\sqrt{x-5}=0\) (Đ/K \(x\ge5\))
\(\Rightarrow\sqrt{x^2-25}=\sqrt{x-5}\)
\(\Rightarrow\left(\sqrt{x^2-25}\right)^2=\left(\sqrt{x-5}\right)^2\)
\(\Rightarrow x^2-25=x-5\)
\(\Rightarrow x^2-x=-5+25\)
\(\Rightarrow x.\left(x-1\right)=20\)
\(\Rightarrow x.\left(x-1\right)=5.4\)
Vì \(x-1;x\) là hai số tự nhiên liên tiếp nên \(x=5;x-1=4\)
\(\Leftrightarrow x=5;x=5\) (chọn vì t/m điều kiện \(x\ge5\))
Vậy \(x=5\)
Chúc bạn học tốt!!!

 giúp mik nha!
giúp mik nha!






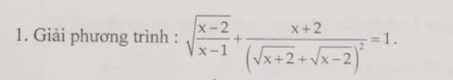


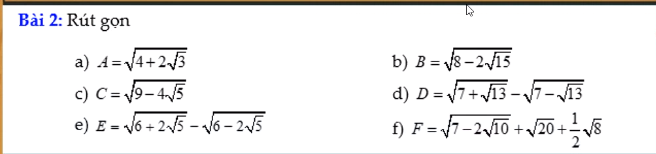 giúp mik với cả 2 bài nha
giúp mik với cả 2 bài nha