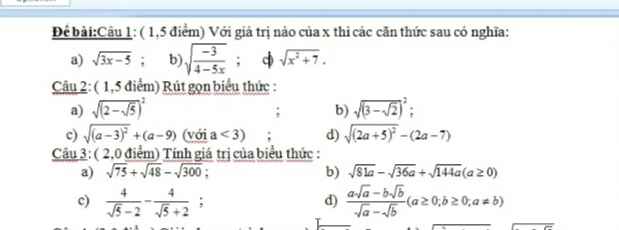
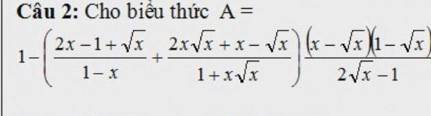Câu 1:
a) ĐK: \(3x-5\ge0\Leftrightarrow x\ge\dfrac{5}{3}\)
b) ĐK: \(-\dfrac{3}{4-5x}>0\) và \(4-5x\ne0\)
\(\Leftrightarrow4-5x< 0\) và \(-5x\ne4\)
\(\Leftrightarrow x>\dfrac{4}{5}\) và \(x\ne-\dfrac{4}{5}\)
c) ĐK: \(x^2+7\ge0\)( luôn đúng ∀x)
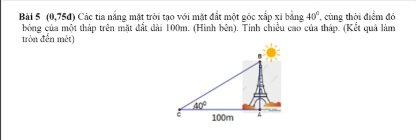
Câu 2:
a) \(\sqrt{\left(2-\sqrt{5}\right)}^2=\left|2-\sqrt{5}\right|=\sqrt{5}-2\)
b) \(\sqrt{\left(3-\sqrt{2}\right)^2}=\left|3-\sqrt{2}\right|=3-\sqrt{2}\)
c) \(\sqrt{\left(a-3\right)^2}+\left(a-9\right)=\left|a-3\right|+\left(a-9\right)=3-a+a-9=-6\)(do a<3)
d) \(\sqrt{\left(2a+5\right)^2}-\left(2a-7\right)\left(1\right)=\left|2a+5\right|-2a+7\)
TH1: \(a\ge-\dfrac{5}{2}\)
\(\left(1\right)=2a+5-2a+7=12\)
TH2: \(a< -\dfrac{5}{2}\)
\(\left(1\right)=-2a-5-2a+7=-4a+2\)
Câu 3:
a: Ta có: \(\sqrt{75}+\sqrt{48}-\sqrt{300}\)
\(=5\sqrt{3}+4\sqrt{3}-10\sqrt{3}\)
\(=-\sqrt{3}\)
b: Ta có: \(\sqrt{81a}-\sqrt{36a}+\sqrt{144a}\)
\(=9\sqrt{a}-6\sqrt{a}+12\sqrt{a}\)
\(=15\sqrt{a}\)
c: Ta có: \(\dfrac{4}{\sqrt{5}-2}-\dfrac{4}{\sqrt{5}+2}\)
\(=4\sqrt{5}+8-4\sqrt{5}+8\)
=16