a) \(2^4+8\left[\left(-2\right)^2:\dfrac{1}{2}\right]^0-2^{-2}.4+\left(-2\right)^2\)
\(=2^4+8.1-\dfrac{1}{4}.4+4\)
\(=16+8-1+4\)
\(=24-1+4\)
\(=23+4\)
\(=27\)
Bài 4:
\(8^{12}\)\(-2^{33}\)-\(2^{30}\) chia hết cho 55
= \(2^{36}\)-\(2^{33}\)-\(2^{30}\)
= \(2^{30}.\left(2^6-2^3-1\right)\)
= \(2^{30}\). 55 chia hết cho 55 (đpcm)
Bài 3:
Ta có: \(5^{1000}=\left(5^2\right)^{500}=25^{500}\)
\(3^{1500}=\left(3^3\right)^{500}=27^{500}\)
Do \(25^{500}< 27^{500}\Rightarrow5^{1000}< 3^{1500}\)
d, \(2^x+2^{x+4}=544\)
\(\Rightarrow2^x+2^x.2^4=544
\)
\(\Rightarrow2^x.\left(1+2^4\right)\)
\(\Rightarrow2^x.17=544\)
\(\Rightarrow2^x=32\)
\(\Rightarrow2^x=2^5\)\(\Leftrightarrow x=5\)










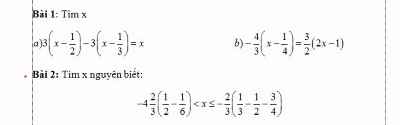 giúp mik giải 2 bài này vs ạ
giúp mik giải 2 bài này vs ạ

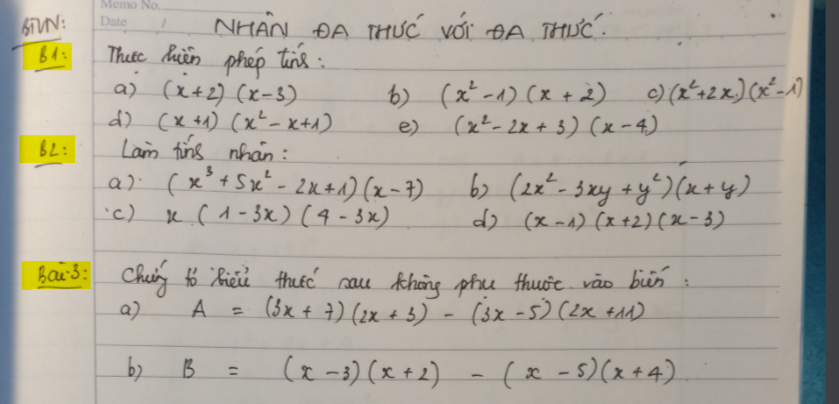

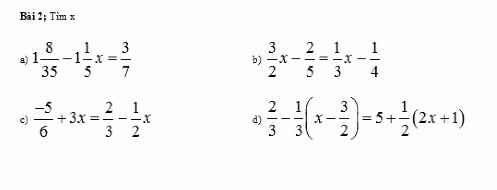
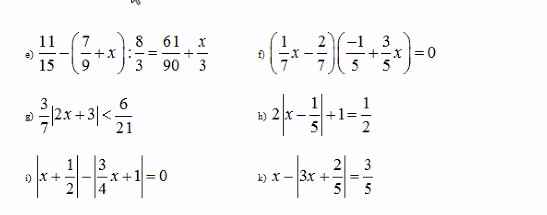
 mn lm giúp mik vs ạ.Mik đang cần gấp ạ.Nhanh ạ
mn lm giúp mik vs ạ.Mik đang cần gấp ạ.Nhanh ạ